
Learn about other kinds of analysis in our Finite Element Analysis Ultimate Cheat Sheet!
THE STUDY OF THE DYNAMIC PROPERTIES OF A SYSTEM IN THE FREQUENCY DOMAIN
THE FIELD OF MEASURING, OR CALCULATING, AND ANALYZING THE DYNAMIC RESPONSE OF STRUCTURES, FLUIDS AND/OR OTHER SYSTEMS DURING EXCITATION
Natural vibrations are caused only by internal forces, and in the absence of external force.
They are a result of the forces contained in the structure: inertial, damping and elastic forces.
They vibrate at one or more natural frequencies.
Natural frequencies are unique dynamic properties of structures not affected by external forces.
The natural frequency of a structure can be found using the mass, damping and stiffness of the structure.
Forced vibrations are caused by the acting of external force on a structure.
If the external force is periodic, the system vibrates at the same frequency as the force.
If the excitation frequency of the external force and the natural frequency of the structure match or are similar, resonance will occur.
Reduces the vibration of a structure.
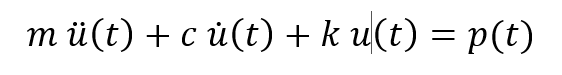
m = mass ; c = damping coefficient ; k = elasticity constant ; p(t) = acting load
u(t) = displacement response ; ὐ(t) = velocity response ; ü(t) = acceleration response
m ü(t) = Inertial Force ; c ὐ(t) = Damping Force ; k u(t) = Elastic Force
Resonance is a phenomenon that occurs in structures when the forced frequency of external forces matches the natural frequency of the structure.
Resonance causes the vibration response of a structure to greatly amplify, due to the superposition of external and internal vibrations.
If the working frequency of an object is near its natural frequency, vibrations and noise increase due to resonance, potentially destroying the structure.
FINDING THE NATURAL FREQUENCY OF A STRUCTURE IN NATURAL VIBRATION
Time taken for one reciprocating motion
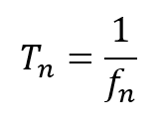
Number of vibrations per second
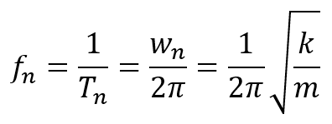
Increase in mass reduces the natural frequency.
Increase in stiffness increases the natural frequency.
Angular velocity corresponding to frequency
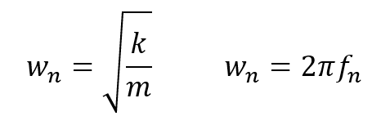
Examine whether or not natural frequency is within the range of operating frequency of external excitation.
Normally, the natural frequencies of the three lowest modes are identified. If they are outside of the operating frequency range the structure is judged safe with respect to resonance. Otherwise, resonance may occur.
If the direction of the load is known, examine the mass participation factor and the direction of each mode. In each mode, if the acting direction of the load and of the highest mass participation factor do not match, the mode does not harm the stability of dynamic behavior. If they match, the design must be modified to avoid resonance.
To be safe, the natural frequency of the structure should be no more than a third of or at least three times the operating frequency.
Use the characteristic of natural frequency: it is proportional to the stiffness and inversely proportional to the mass. Increasing stiffness or reducing mass of a structure will increase the natural frequency, and vice versa.
When reinforcing a structure to increase stiffness, it is most effective to find and reinforce the part with high deformation energy in the mode of interest. Reinforcements that increase stiffness will lower deformation energy and increase the natural frequency.
Mode shapes are only important in terms of the deformation shape; the size of the deformation is not important.
Overall vibration behavior over a whole period should be examined through animation.
With a dynamic shape that vibrates periodically, the direction of a stationary deformation shape has no significance.
Use natural frequency and mode shape through mode superposition.
Identify sufficient modes to allow dynamic analysis.
Verify a total mass participation factor of at least 90%.
Identify time increment for time response analysis.
Identify frequency range of interest and set frequency increment.
Natural Frequency:
If modal analysis shows the possibility of resonance of a structure, the design can be modified so that the natural frequency of the structure is no more than 1/3 of the operating frequency, or at least 3 times greater.
Mode Shape:
Mode shapes help identify natural frequencies having large or small impacts on the design.
If the direction of the mode shape and the acting load are different in a mode, the impact of natural frequency in the given mode is small.
| |
Speaker : Gabriel Roade Category : Mechanical Software : midas MeshFree Date : 2018-09-03 |

Search
Featured Resources
Structural Analysis
What Is Linear Static Analysis?
Read more >

Dynamic
Finite Element Analysis Types: The Ultimate Cheat Sheet
Read more >
Project Application
Boundary Conditions of Eigenvalue Analysis [IAD 4]
Read more >

Structural Analysis
The Future of Finite Element Analysis: MeshFree
Read more >