Expert Tips: Material Properties' Time Functions
Author: Seungwoo Lee, Ph.D., P.E., S.E.
Publish Date: 29 Mar, 2021
In the blog article intro to Time-dependent Analysis for Concrete Structures, we have touched upon the importance of construction stage analysis for concrete structures. The material time function can be plotted and inputted into analysis software like midas Civil to simulate their changing material behavior in various stages of the construction. This article will go over the process of calculating various parameters that contribute to the shape and location of the material's time functions.
- How to Obtain the Time Function of the Modulus of Elasticity?
The modulus of elasticity of concrete at age t may be estimated by:
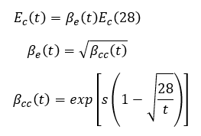
with s being a coefficient depending on the type of cement; s is equal to 0.2, 0.25, and 0.38, respectively, for rapidly hardening high-strength cement, normal and rapidly hardening cement, and slowly hardening cement.
Assume normal and rapidly hardening cement, therefore s = 0.25.
The modulus of elasticity of concrete at age 28 days, Ec(28), for normal-weight concrete can be estimated by:
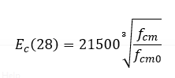
where fcm0 = 10 MPa.
When the mean compressive strength fcm is not known, Ec(28) may be estimated from the characteristic compressive strength, fck at 28 days by the equation:
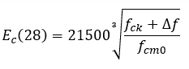
where Δf = 8 MPa.
These equations apply when quartzitic aggregates are used. For other aggregates, multiply Ec(28) by a factor varying between 0.7 and 1.2. These equations give the tangent modulus of elasticity, which is equal to the slope of the stress-strain diagram at the origin.
When the modulus of elasticity is for used in an elastic analysis, without considering creep, the value Ec(28) should be reduced by a factor of 0.85 to account for the quasi-instantaneous strain, which occurs shortly (within one day) after loading.
Assume fck = 7 ksi = 48.26 MPa,
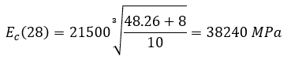
Ec (MPa) can therefore be plotted against time (number of days)below,
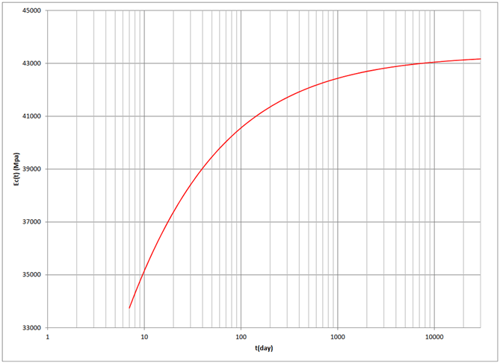
Figure 1. Plot of Ec (t) with characteristic compressive strength fck = 7 ksi at 28 days. CEB-FIP 1.01.xlsm
- How to Determine the Final Modulus of Elasticity of the Concrete?
At t = ∞,

Therefore, the final modulus of elasticity is dependent on the cement type and its compressive strength.
- How to Determine the Time Function of Creep Coefficient?
We recall the definition of the creep coefficient from the article Intro to Time-dependent Analysis for Concrete Structures as the ratio of creep at time t to the instantaneous strain due to constant stress introduced at time t0. MC-90 gives a coefficient φCEB(t, t0), which is equal to φ(t, t0) divided by
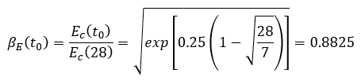
The equation given by MC-90 for φCEB is adjusted below to give the creep coefficient φ(t, t0),
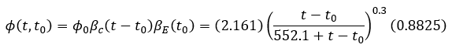
where βc is a coefficient describing the development of creep with time after loading; φ0 is a notional creep coefficient given by:
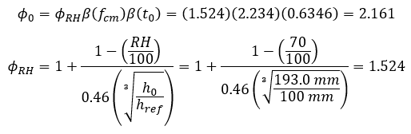
where href = 100mm, RH is relative humidity and assumed as 70%.
The symbol h0 (mm) is the notional size of member defined by
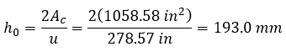
where Ac and u are the area and perimeter of the cross-section of the considered member that is in contact with the atmosphere.
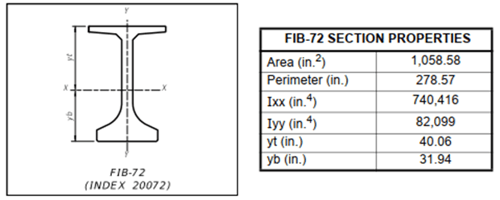
Figure 2. Section properties of FIB-72 I-beam.
Assume the section is FIB-72, and the age at loading t0 = 7 days.
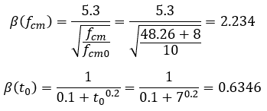
Development of creep with time is expressed by:
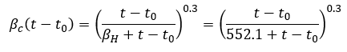
βH is a function of the notional size h0 and the relative humidity, RH:
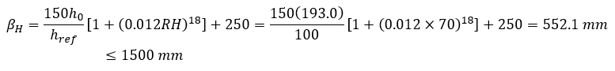
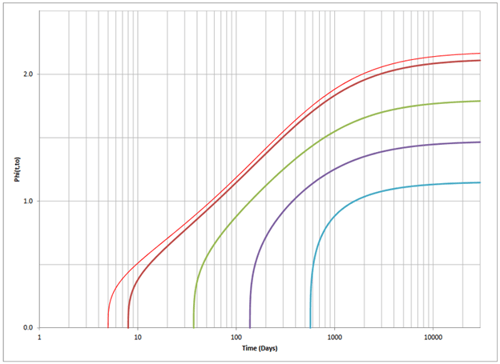
Therefore, we obtain the time function for the creep coefficient and plot it below with respect to time.
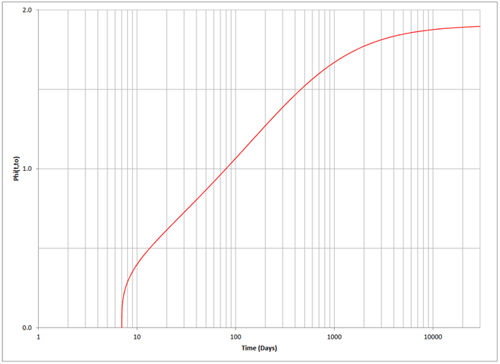
Figure 3. Plot of φ(t, t0) with fck = 7 ksi at 28 days, t0 = 7 days, RH = 70%, h0 = 193.0 mm. CEB-FIP 1.01.xlsm
- What is the Final Creep Coefficient?
At t (or t – t0) = ∞,
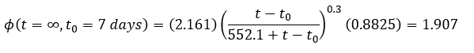
Therefore, the final creep coefficient is dependent on relative humidity, notional size of member, concrete strength, and age at loading.
- How to Determine the Time Function of Shrinkage?
When does shrinkage start? Shrinkage starts at time ts (days) when curing is stopped. On the other hand, concrete starts to swell at time ts when immersed in water. The shrinkage or the swelling at any time t (days) may be estimated by:
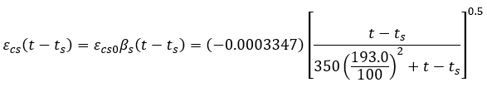
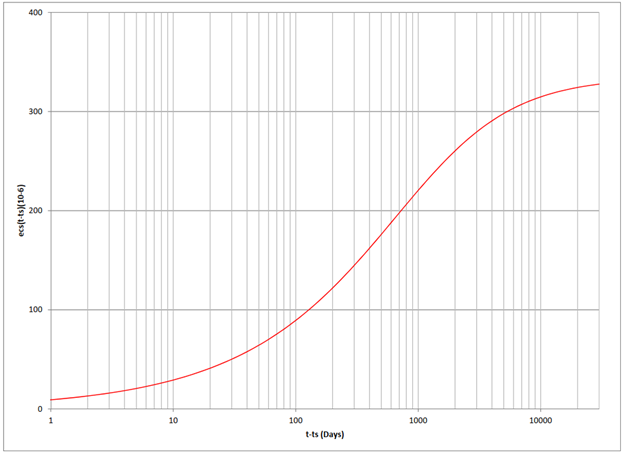
Assume ts = 3 days, where εcs0 is the notional shrinkage given by:
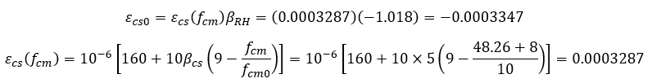
with βcs equaling 4, 5, or 8, respectively, for slowly hardening cement, for normal or rapidly hardening cement, and for rapidly hardening high-strength cement.
For 40% ≤ RH < 99%,
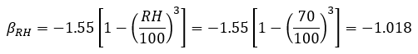
For RH ≥ 99% (immersed in water), βRH = +0.25, with positive βRH indicates swelling.
βs(t − ts) is a function describing the development of shrinkage or swelling with time, given by:
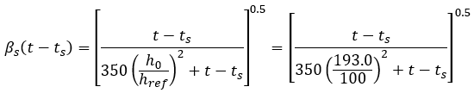
Therefore, we obtain the time function of shrinkage and plot it below with respect to time,
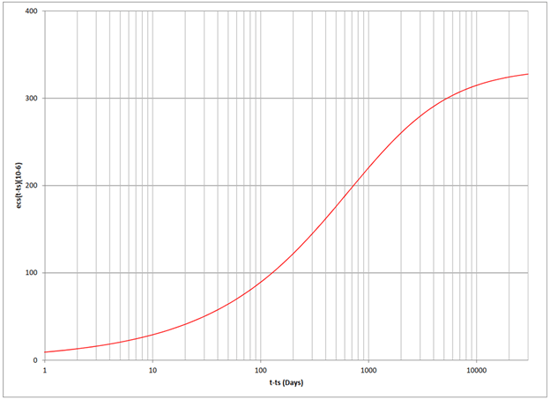
Figure 4. Plot of εcs with fck = 7 ksi, normal and rapidly hardening cements, ts = 3 days, RH = 70%, h0 = 193.0 mm. CEB-FIP 1.01.xlsm
- What is the Final Shrinkage?
At ts (or t – ts) = ∞,
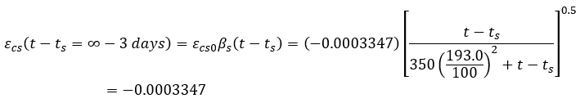
The final shrinkage is dependent on the type of cement, concrete strength, and relative humidity. Final shrinkage is dependent on the notional size of a member.
Finally, it should be mentioned that the code equations above for the creep coefficient φ(t, t0) are valid for a mean temperature of 20 °C (68 °F), taking into account seasonal variations between −20 °C (-4 °F) and + 40 °C (+104 °F). When the prevailing temperature is higher or lower than 20 degree Celsius, the effect of temperature on the maturity of concrete may be accounted for.
Add a Comment