Expert Tips: Creep Analysis 5

Creep Analysis 5 MIDAS Example

In this article, the previous method explained in Creep Analysis 4 is applied to a real-world bridge and compares the output with MIDAS’.

Consider a two-span bridge as shown below.

Two-span bridge

Stage 1

Stage 2

The typical section is as shown.

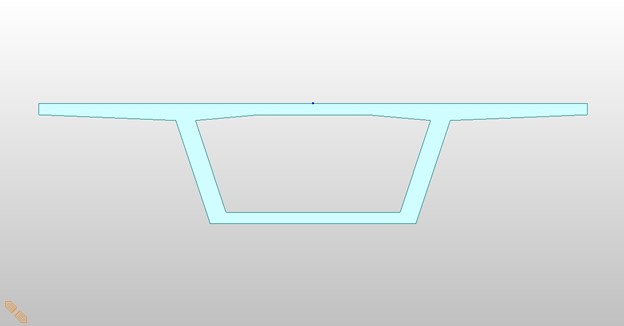Typical section

Section properties are:

Material properties are:

Creep Coefficient

Elastic Modulus (MPa)

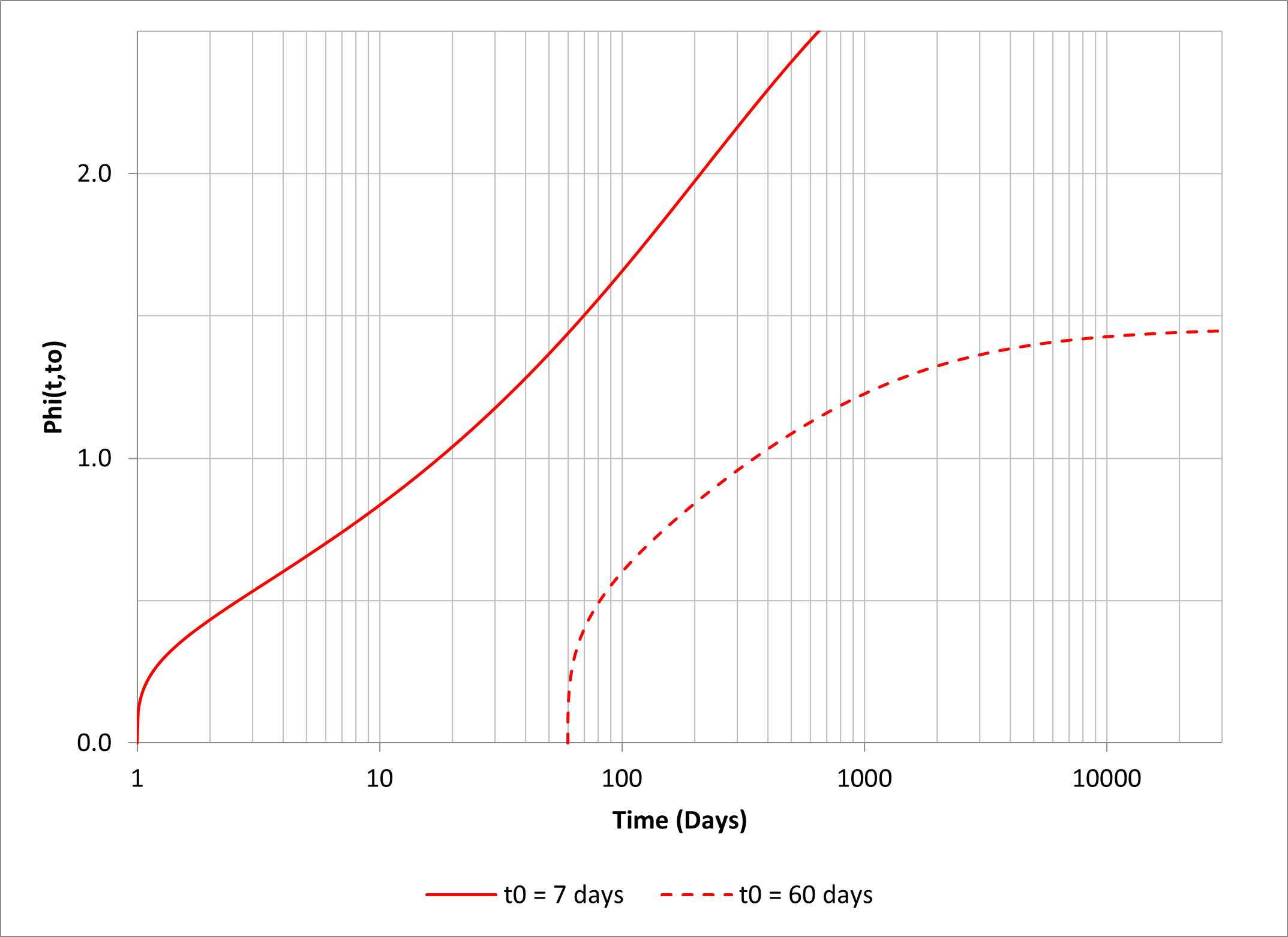
From the graph,

φ(∞, 7) = 2.19                                   χ(∞, 7) = 0.74                                    φ(60, 7) = 0.975

φ(∞, 60) = 1.46                                 χ(∞, 60) = 0.82.

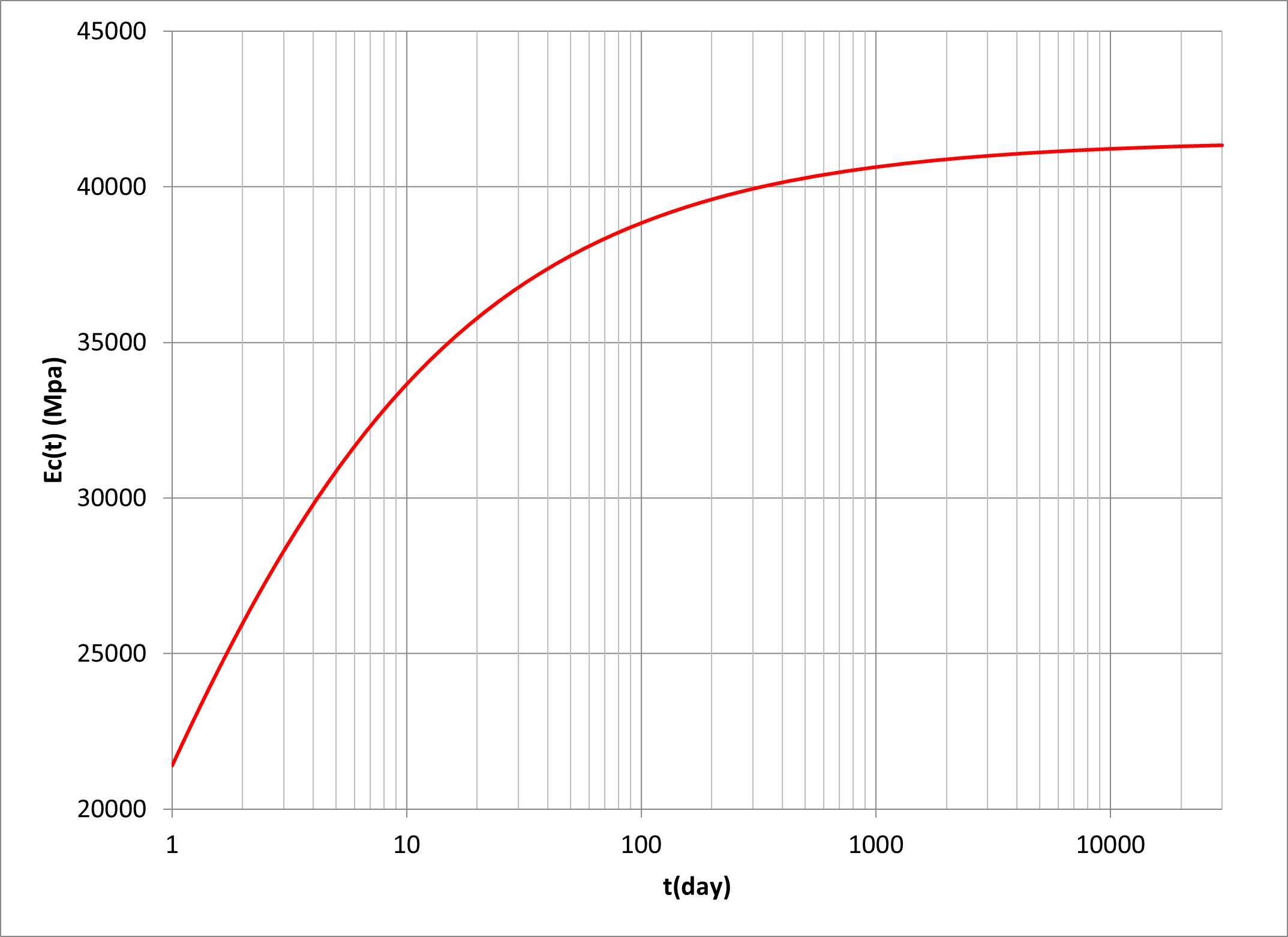
Ec(60)/Ec(7) = 1.040/0.882 = 1.179.

At time t₁ = 60 days, the member end forces due to self-weight at span 2 can be calculated as below. Note that Ec(60)/Ec(7) = 1.179. (MIDAS file ex.2C)

[Member End Force] = [Stiffness]{Displacement} + {Fixed End Force}

[Stiffness]{Displacement} = [Member End Force] - {Fixed End Force}

Analyze two-span continuous beam for these member end loadings. Note that the section properties are as below and the loading directions may not be identical for each program. (MIDAS file ex.2D)

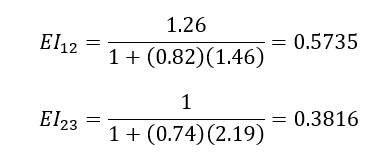
Results (ft, kips)

Finally, the member end forces are:

Span AB

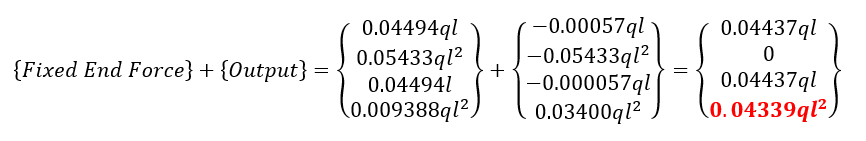
Span BC

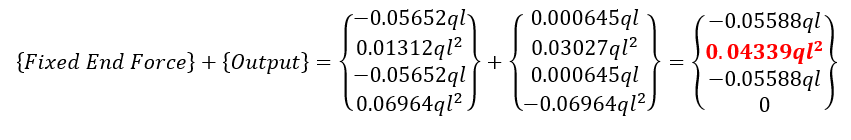
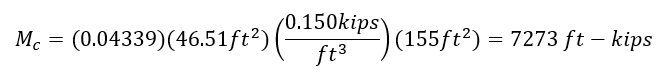
Check this result with MIDAS output (MIDAS file ex.2E).

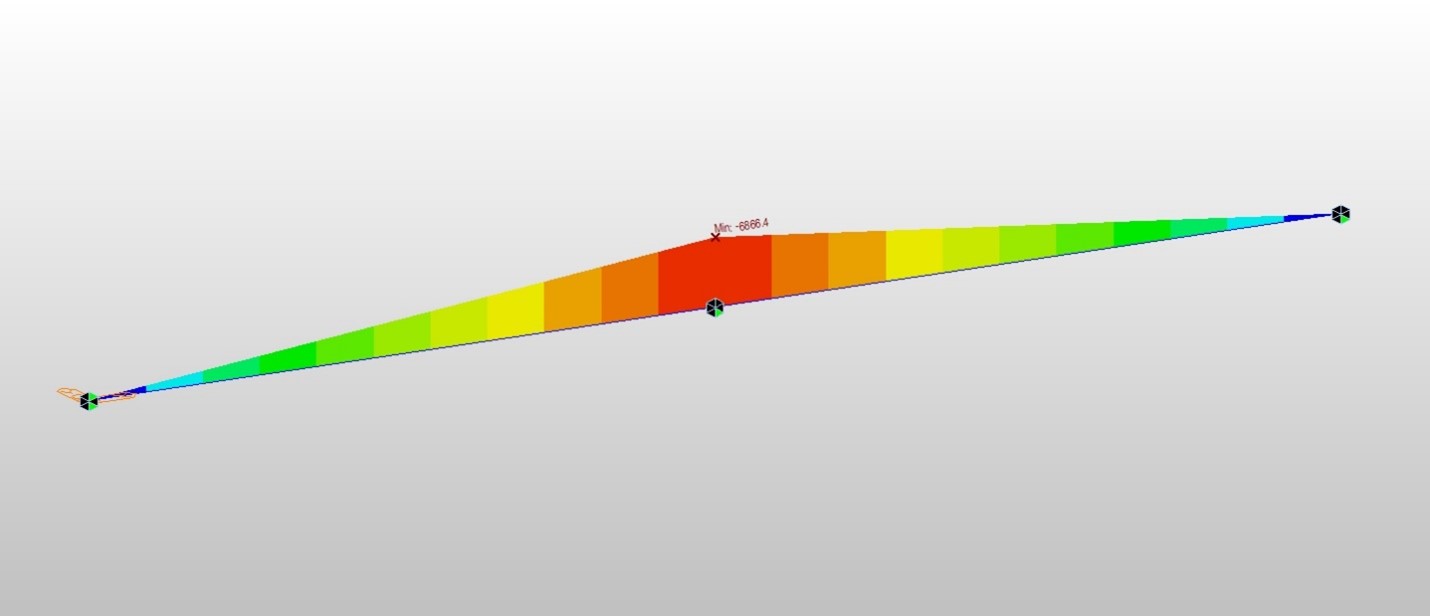
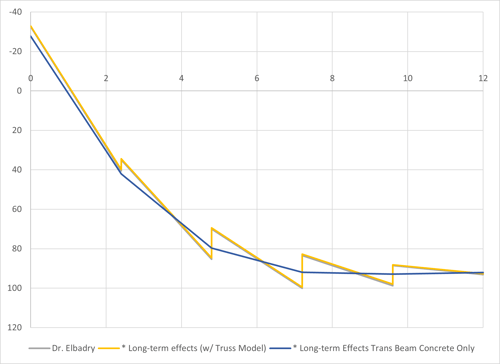
Creep secondary moment (ft-kips)

Construction analysis from MIDAS gives creep secondary moment at pier 2 as 6866 ft-kips. The error between the two methods is 6% and again we do not know where these differences come from. However, considering the uncertainty of creep itself, the author believes this error is acceptable in practical design.