Expert Tip: How to Perform Time-dependent Analysis

How to Perform Time-dependent Analysis?

Mainly there are two ways to perform the time-dependent analysis. One is the time-step analysis and the other is the age-adjusted method.

The age-adjusted method is a simplified one and can consider the long-term effects with only a one-step analysis. Of course, this is an approximate way to consider the long-term effects, but the creep itself is an approximation anyway. The results from the age-adjusted method are reasonable in many cases.

The author prefers the time-step analysis. The time-step analysis is nothing more than to do the same calculation again and again. This is painful for humans but computers are very good for these repeated calculations. The time-step analysis is to divide the time into shorter durations of time-steps and repeat the same analysis. All calculations are done by the computers and extra efforts comparing to the age-adjusted method is nominal. (We need computers anyway even for the age-adjusted method.)

As always, before starting theory discussions, start with a simple example.

• Post-tensioned section Example (Example 2.2 from Concrete structures, 3^rd ed., by Dr. Ghali, et al.)

A prestress force P = 1400 kN and a bending moment M = 390 kN-m are applied at age t₀ = 5 days on the rectangular post-tensioned concrete section shown in Figure 1. Calculate the stresses, the axial strain and curvature at age t₀ and t = ∞ given the following data: E_ns = E_ps = 200 GPa; f’c = 5 ksi, RH = 70%, t_s = 3 days. The dimensions of the section and cross-section areas of the reinforcement and the prestress duct are indicated in Figure 1.

Assume that the intrinsic relaxation, ∆σ_pr∞ = −115 MPa and the characteristic tensile strength of the prestressed steel, fptk = 1770 MPa.

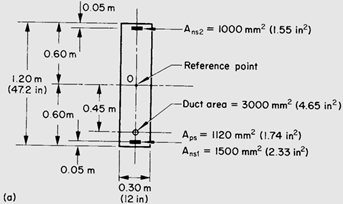
Figure 1. Cross-section dimensions of the post-tensioned section. 

Step1) Elastic strain at t₀

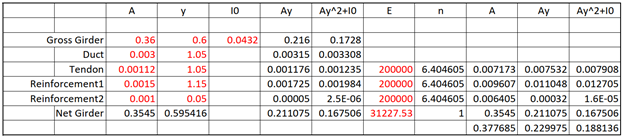
The axial strain at O and curvature is

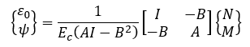
When the reference point O is chosen at the centroid of the section, B = 0, and the equation takes the more familiar form

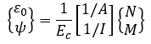
In this example, the reference point O is chosen at the top of the section. 

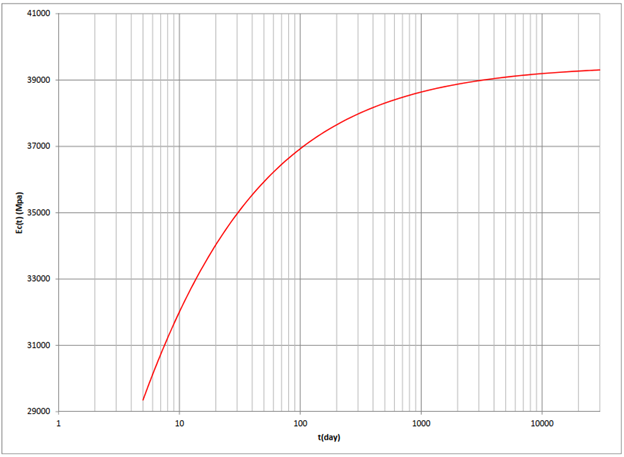
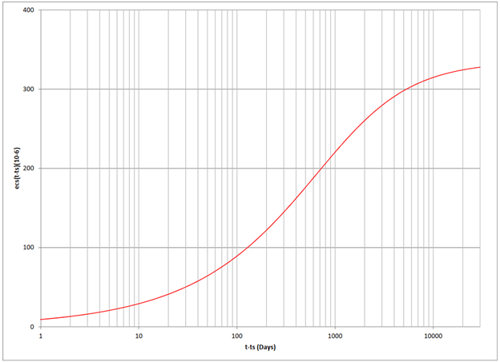
Figure 2. Ec(5 days) = 29352 MPa

Table 1. Section property (Reference point is section top, t = 5 days)

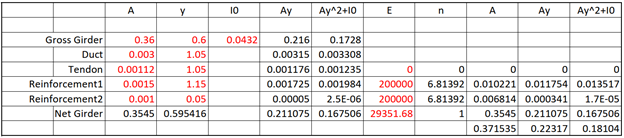
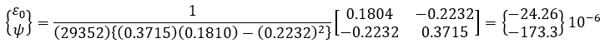
Step2) Strain at t = 8 days

Ec(8 days) = 29352 MPa

Table 2. Section property (Reference point is section top, t = 8 days)

Restrained strain due to concrete creep

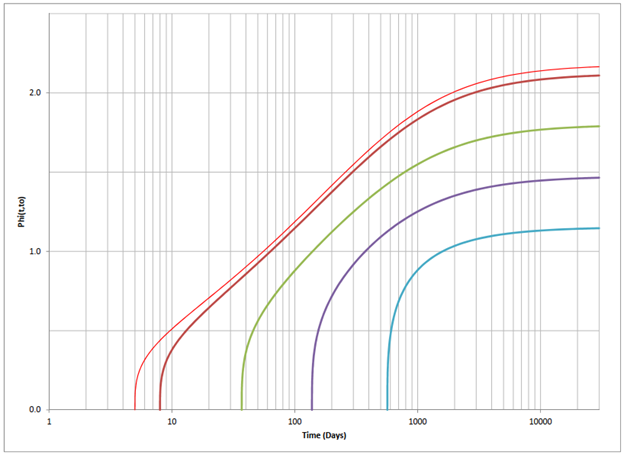
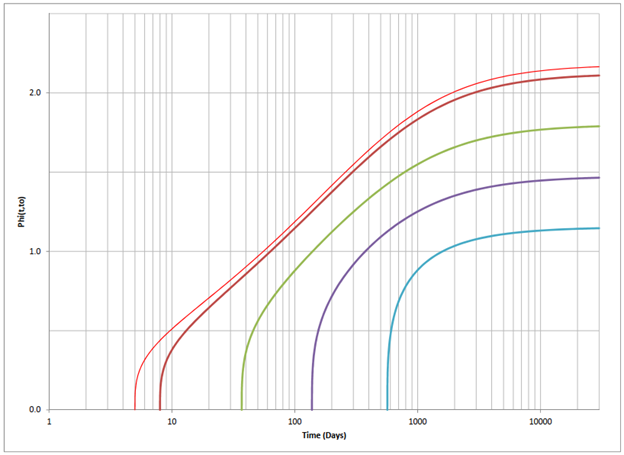
Figure 3. φ(t,t₀) (t₀ = 5, 8, 37, 128, 567 days).

φ(8,5) = 0.4383

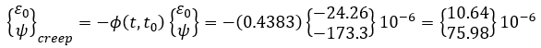
Restrained strain due to concrete shrinkage

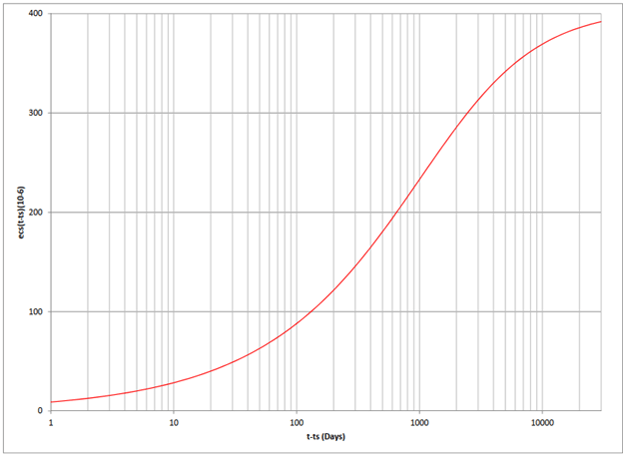
Figure 4. Restrained strain due to concrete shrinkage

ε_sh(8,3) = -20.14(10^-6)

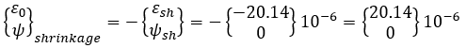
Restrained strain due to strand relaxation

Reduced relaxation value:

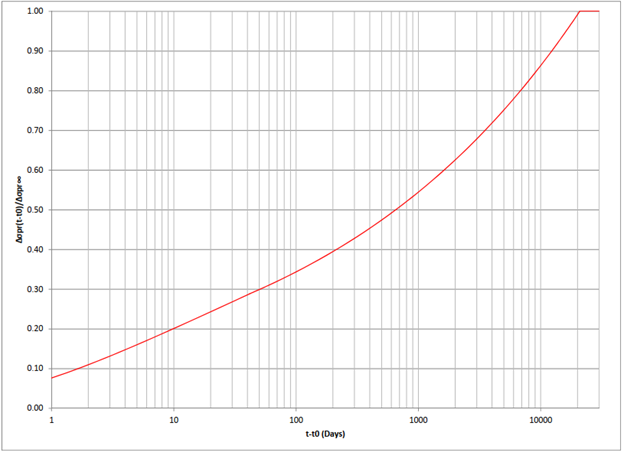
Figure 5. Reduced relaxation value.

(τ – t₀) = 8 – 5 = 3 days = 72 hrs < 1000 hrs,

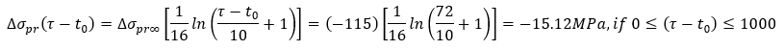
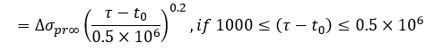
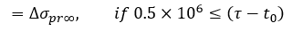
Assume χ_r = 0.9581,

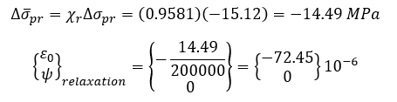
Restraining force

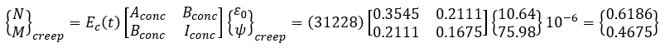
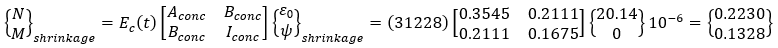
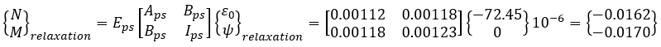
Strain due to restraint

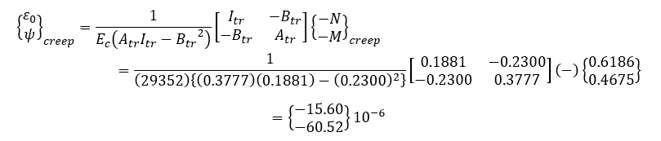
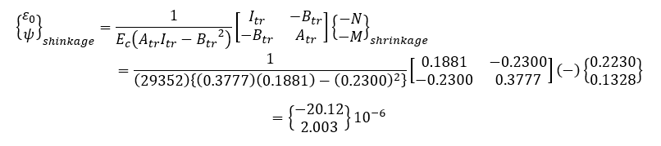
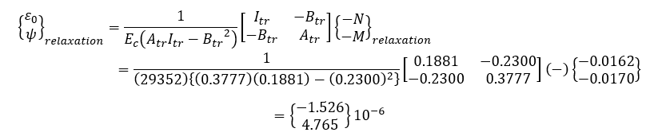
Check for χr 

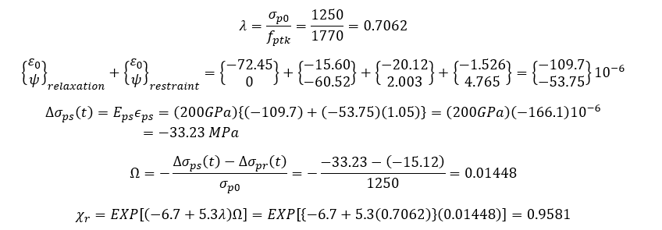
The calculated value of χ_r matches with the assumed value. No further iteration is needed. Repeat the same calculations for the next time steps.

• Discussion

Midas Civil File for This Example

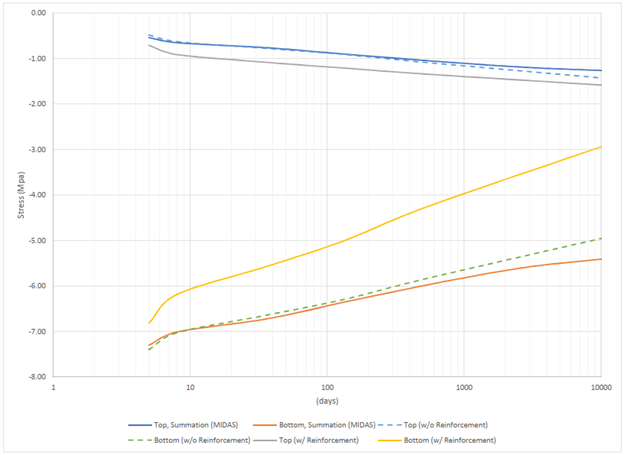
Figure 6. Concrete stresses at top and bottom.

Figure 6 shows top and bottom concrete stresses from this article and Midas Civil. Can be seen some differences at the bottom fiber and this is because reinforcements would support portions of external load and prestress. Also, stresses are transferred from concrete into reinforcement as time passes. The dashed line shows stresses without considering reinforcements and well matches with Midas Civil.

It can be seen that if we use the stress value directly from the computer output, we do need some levels of adjustment to consider the effects of reinforcements.

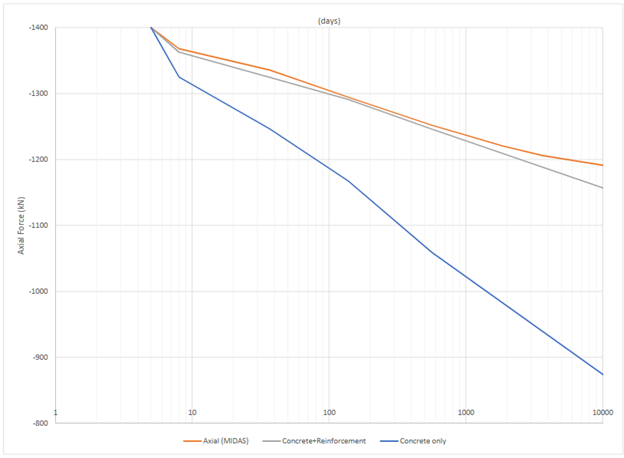
Figure 7. Concrete axial force

Figure 7 shows concrete axial force from Midas Civil and this article. As time passes, portions of concrete axial force are transferred into reinforcements and these effects can not be ignored.

• Closure

• • • As time passes, portions of concrete forces/stresses are transferred into reinforcements. In other words, the absolute values of concrete forces/stresses are reduced and those of reinforcements increase.
      

• • • Most general-purpose programs can not consider these reinforcement effects and we do need to interpret computer output. These effects are more severe for deflection calculations.

• • • To perform the time-step analysis, we have to define the time of infinity. Some programs can consider the time of infinity as t = ∞, however, most general-purpose programs require defining the time of infinity from the user. In this example, φ(∞,5) = 2.1787 which is approximately corresponding t = 1500 years! Considering the uncertainty of creep itself, these levels of precise calculations may be justified. For t = 30 years, φ(30 years, 5 days) = 2.1427, which is 98% of φ(∞,5) = 2.1787, should be enough. For authors view, even when t = 4 years, φ(4 years, 5 days) = 1.9604, which is 90% of φ(∞,5) = 2.1787, might be enough.

• • • The important one is how many and how to divide time steps. Creep, shrinkage, and relaxation coefficients are assumed to be constant within a single time step. These coefficients vary continuously and even not linear. This is why we do need to divide time steps into shorter duration. Computers blindly perform time-dependent analysis and give output without time division, without asking us nor judging whether the output is reasonable or not.

The number of time-division mainly depends on past experiences or iteration. From past experiences, 5 to 10 divisions may be reasonable under the constant loadings.

Equal time division is not efficient because creep develops more rapidly during the early steps. There are many ways to consider these effects, and one of these is to assume the time division as a geometric sequence. The author prefers to divide the time steps corresponds to equal creep coefficients.

• • • Comparing to creep and shrinkage, relaxation effects are less significant. We need iteration to calculate reduced relaxation. The iteration itself is quite simple and the convergency is very fast, but these levels of detailed calculation may not be necessary for practical design.

• • • For indeterminant structures, more consideration is needed and will be discussed later.

Editor: JC Sun

jsun@midasoft.com