Expert Tip: Finite Element Method Basics 4
Author: Seungwoo Lee, Ph.D., P.E., S.E.
Publish Date: 20 Jan, 2023
In the FEM, the most critical question is “how many meshes do we need to get the correct (or reasonable) results?”
Most elements within the commercial programs have been tested and verified that they are converged with element number increases. This statement seems to be given, but not true for all elements. Theoretically, we can get the correct results if we have an infinite number of elements, but this is not feasible. So we have to decide the number of elements with the allowable error.
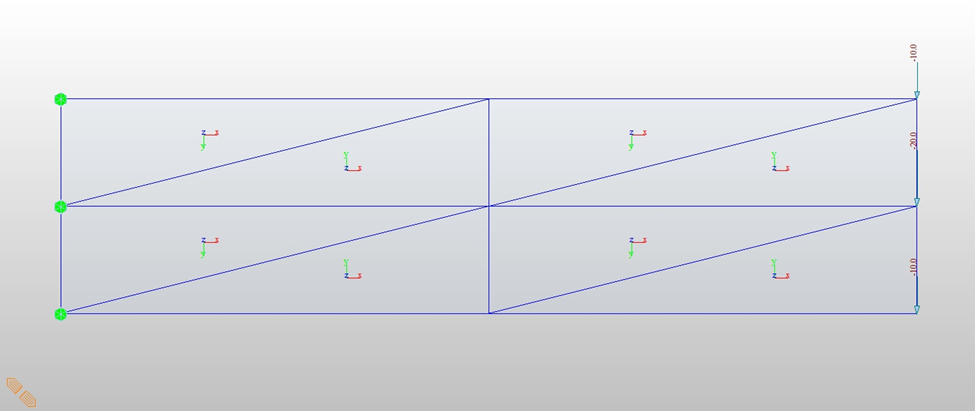
Let’s go back to the linear strain triangle element. Say, we have three models with the same problems, 8 elements, 18 elements, and 32 elements.

8 linear strain triangle elements
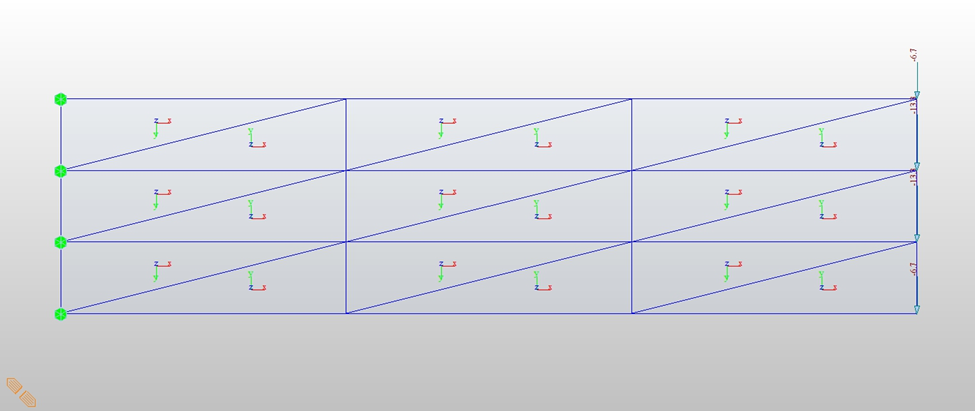
18 linear strain triangle elements
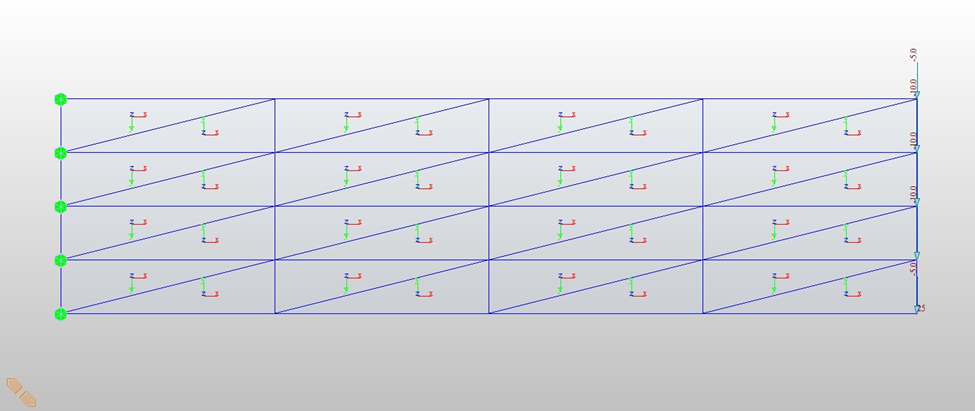
32 linear strain triangle elements
The results are shown below.
|
|
deflection (in) |
stress (ksi) |
|
|
|
|
|
8 triangular elements |
0.0637 |
10.0 |
|
18 triangular elements |
0.111 |
20.8 |
|
32 triangular elements |
0.156 |
31.4 |
|
exact |
0.341 |
80 |
Suppose we do not know the exact results, Δ=0.341 in and σ=80 ksi and we performed only for 32 elements case. We got Δ=0.156 in and σ=31.4 ksi.
How can we be sure these are correct (or reasonable) results?
How can we decide whether we need more refined mesh or not?
Is there any way we can estimate the correct value based on what we got from FEM, even if they are somewhat approximate?
There is a classical method called Richardson’s extrapolation formula to estimate exact values based on two FEM results (S.H. Crandall, Engineering Analysis, McGraw-Hill, NY, 1956). However, this formula has some restrictions and uncertainties, as can be imaged.
The other easy way to predict the correct value was proposed by Dr. Cook, et al (Concepts and Applications for Finite Element Analysis, 4th Ed.).
Assume we performed for more cases, with 8 and with 18 elements. The following two graph show tip deflection and stress at fixed support. The horizontal axis represents 1/√(number of elements).
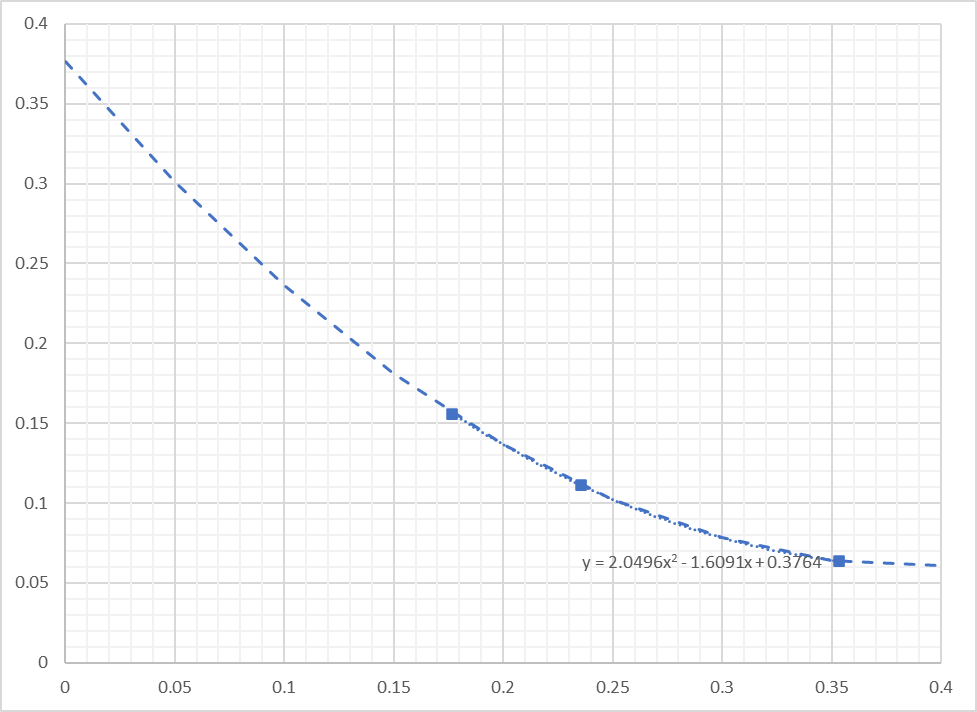
1/√(number of elements) vs tip deflection (in.)
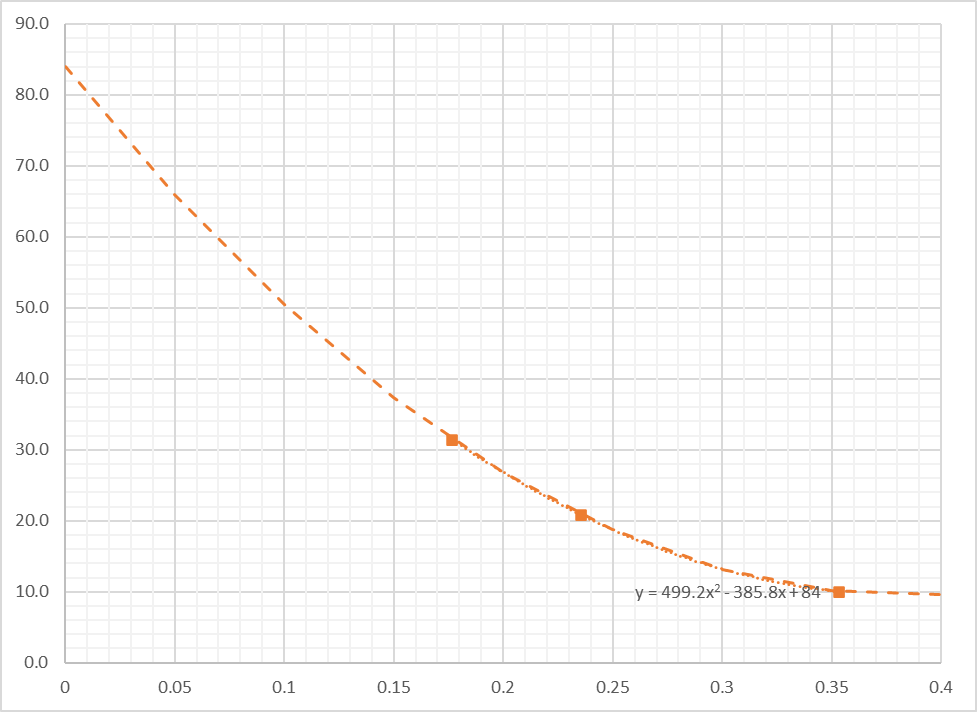
1/√(number of elements) vs stress at fixed support (ksi)
Dashed lines represent regression with 2nd order. At horizontal axis=0, which corresponds to an infinite number of elements (1/√(0) = ∞), the deflection and stress are around 0.38 in. and 84 ksi. These are not exact, but much better than we estimated with 32 elements and may be good to use for practical engineering problems. Based on this study, we can increase element division to get reasonable results.
This method may look perfect. But, as Dr. Cook commented, “the extrapolated result is remarkably good, although such a good result may be somewhat fortuitous”.
Also, we may have some more questions.
Why do we apply the horizontal axis as 1/√(number of elements), not 1/(number of elements), nor 1/(number of horizontal elements), etc?
Why do we apply 2nd order regression, why not linear regression, not log regression, etc?


Add a Comment