Expert Tip: Concrete shear design based on AASHTO LRFD 5

Author: Seungwoo Lee, Ph.D., P.E., S.E.
Publish Date: 20 Jun, 2023
Solving the previous example from full iteration
Now it’s time to solve the previous example from full iteration. For simplicity, interaction with flexure is not considered. In other words, it is assumed that the status is in a pure shear condition which rarely exists in the real world.
Assume that both tensile and compression reinforcements are 3-#11 (4.68 in2) and stirrups are 2-#3@6 in.
Detailed calculation is only shown for ε1=0.002 case.
Step 1) choose ε1=0.002
Step 2)
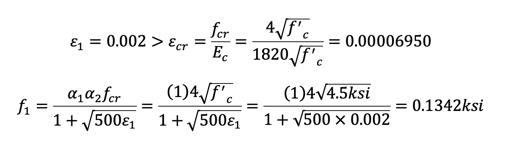
Step 3)
![]()
Step 4) estimate θ=36.30°
Step 5) estimate fv=35.75 ksi
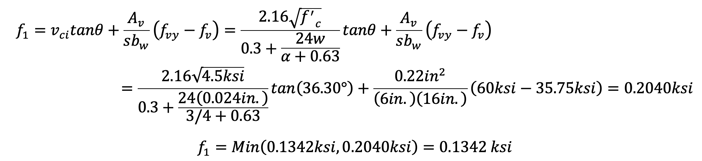
Step 6)
From vertical equilibrium,
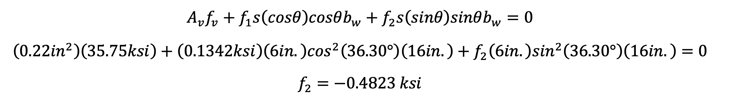
From Mohr’s circle,
![]()
From definition,
or
Step 7)
Step 8)
Step 9)
Step 10)
Step 11)
Step 12)
Repeat Steps 5) to 12) as required.
Step 13)
Otherwise, repeat Steps 4) to 13) as required.
Step 14)
Otherwise, reduced f1 and repeat Steps 6) to 14) as required.
Similar calculations can be done for other values of ε1. It would be helpful if the following strain cases are included as the minimum, 1) cracking strain, 2) stirrup yield strain, and 3) concrete crush strain.
Shear response summary
For this analysis, we can get some useful information.
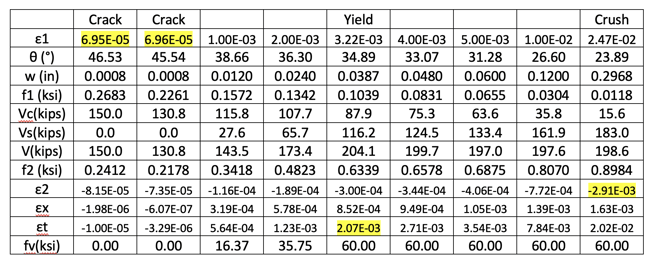
ε1 vs θ (°)
With the increase of principal strain ε1, the crack angle θ tends to decrease.
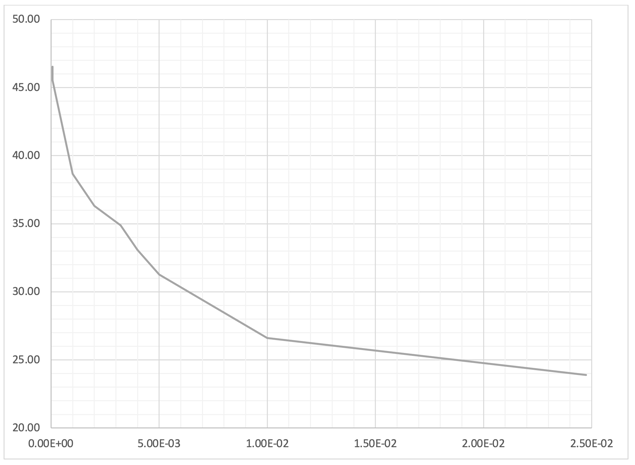
ε1 vs Vc, Vc+Vs (kips)
With the increase of principal strain ε1, resistance from concrete Vc tends to decrease, but resistance from reinforcement tends to increase. The maximum resistance occurs at the yielding points.
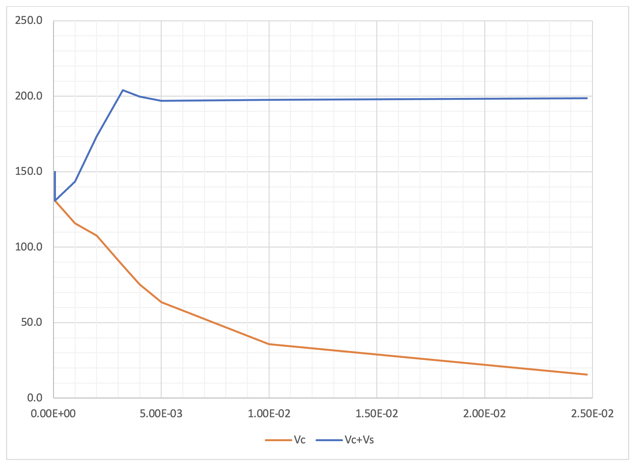
ε1 vs f1, f2 (ksi)
With the increase of principal strain ε1, principal tensile stress f1 tends to decrease, but principal compressive stress f2 tends to increase.
Conclusion
From the full iteration analysis, we can see that the shear resistance is around Vc+Vs=200 kips, φVn=180 kips which is larger than the demand Vu=157 kips. Considering we reduced stirrup spacing from a maximum of 7.7 in. to 6 in., these results look very reasonable. Also, the crack angle θ=36.30° at the stirrup yielding condition is close to θ=36° from the design table.
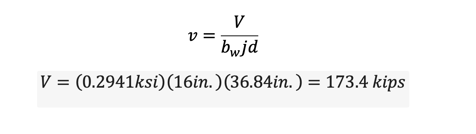

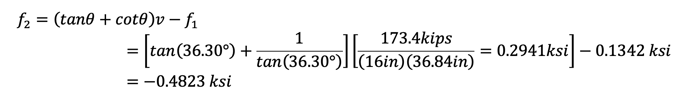
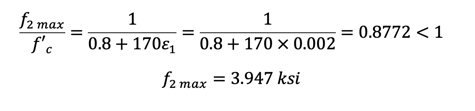
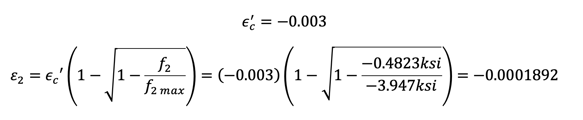
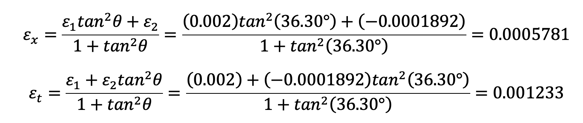
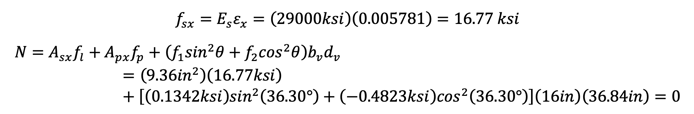
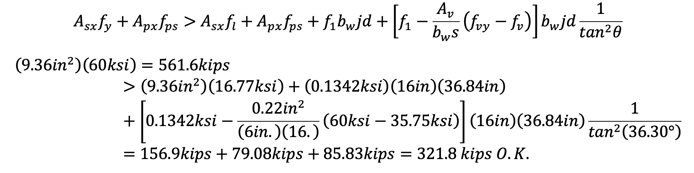
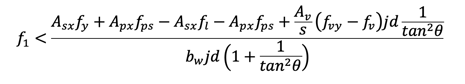




Add a Comment