Basic Finite Element Mesh Explained

Author: JC Sun
Publish Date: 28 Dec, 2021
To ensure stable analysis performance and reliable result approximation, meshing is important. Meshing is the process to create finite elements and to connect those elements to formulate a set of functions. Finite elements are created by separating the known geometry with imaginary lines, and the elements are then connected with each other by specifying nodal connectivity at the element boundaries. Every element can be represented by a set of matrices (shown later), and connecting the elements essentially compiles the individual matrices into one structural matrix.
- What is Finite Element Mesh?
Any non-time-dependent finite element analysis contains the following steps,
-
- Meshing
- Assigning boundary conditions
- Applying loads
- Numerical analysis
- Postprocessing
To ensure stable analysis performance and reliable result approximation, meshing is important. Meshing is the process to create finite elements and to connect those elements to formulate a set of functions. Finite elements are created by separating the known geometry with imaginary lines, and the elements are then connected with each other by specifying nodal connectivity at the element boundaries. Every element can be represented by a set of matrices (shown later), and connecting the elements essentially compiles the individual matrices into 1 structural matrix.
- Types of Finite Elements
Any non-time-dependent finite element analysis contains the following steps, Based on the shapes, there are the following types of finite elements:
- One-dimensional elements
- Two-dimensional elements
- Three-dimensional elements
In this article, we are going over each type of the finite element listed above, explaining its pros and cons, and when to use each type.
- One-Dimensional Elements
One-dimensional elements (line elements) include bar elements and beam elements, and the difference between the two depends on their load-bearing capabilities. Bar elements are suitable for modeling trusses because their load-bearing capabilities are limited in the axial directions. On the other hand, beam elements are suitable for modeling frames because they can resist bending, twisting, as well as axial forces. A beam that is continuous over two or more supports can usually be modeled using one beam element per span between supports without using several beam elements to model one individual span. Thus, when a one-dimensional element is used for static analysis, the discretization phase of modeling becomes trivial, and for stress analysis, the name “matrix methods of structural mechanics” may be used in preference to “FEA” [1].
To represent a bar in axial tension, shown in figure 1, the following considerations can be made to compile the stiffness matrix.
 Figure 1. A prism bar with one end fixed and the other end subjected to a force P.
Figure 1. A prism bar with one end fixed and the other end subjected to a force P.
A prismatic bar of length L, cross-section area A, and elastic modulus E is subjected to a force P at one end and with the other end fixed. The tensile elongation of the bar can be represented as
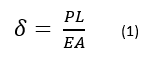 For a two-node bar element, shown in figure 2,
For a two-node bar element, shown in figure 2,
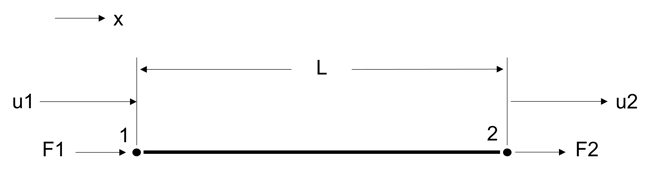
Figure 2. A two-node bar element.
The equilibrium at each individual node gives the following:
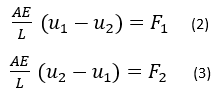
Which can be written in the matrix format as:
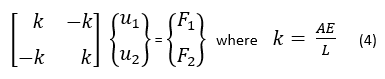
further reduction gives:
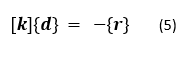
Where [k] is the characteristic matrix (stiffness matrix), {d} is the displacement vector, and {r} is the loads associated with each individual node.
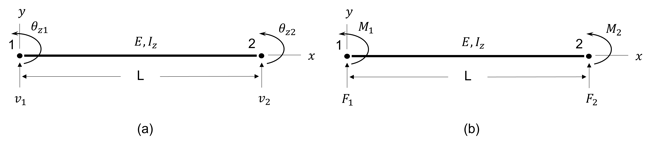
Figure 3. A beam with two nodes (a) with two degrees of freedom at each node, translational in y and rotation in z, (b) with vertical loads and rotational moments at each node.
Figure 3 shows a beam element with two nodes. Each node is subjected to two degrees of freedom (figure 3a) and two nodal forces (figure 3b). Using the Euler-Bernoulli beam theory, the following matrix equation can be formed:
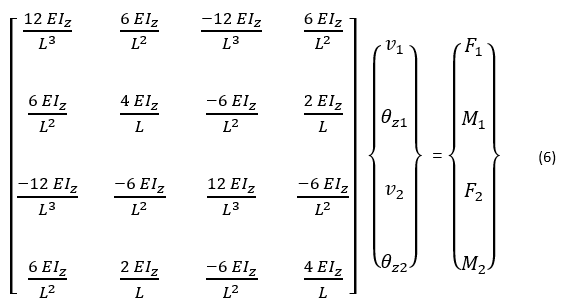
The same element stiffness matrix can be obtained by calculating using interpolation and shape functions,
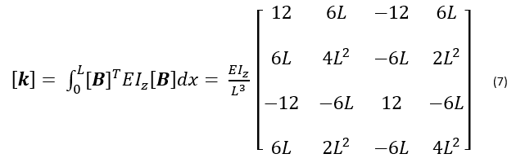
Where [B] is the strain-displacement matrix obtained from the shape functions [N]. We can also use shape function interpolation to obtain the stiffness matrix of 2D and 3D elements as well, as shown later in the article.
Line elements are widely used in general structural analysis to obtain an overview of structural behavior, as well as in the detailed analysis in conjunction with other types of elements as connections, stiffeners, etc. In bridge engineering, the general structural analysis using 1D elements gives engineers a comprehensive understanding of the bridge structural behavior, as well as provides member forces and moments for design code checking for various standards.
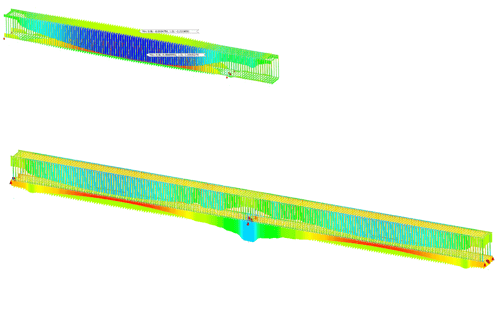
However, to obtain more insights about localized structural zones, or when analyzing complex bridge geometries, local refinement would be required. To satisfy those higher analysis requirements, two-dimensional elements and three-dimensional elements offer better result approximation. Figure 4 (left) shows the general analysis result using the 1D element, and figure 4 (right) shows the refined analysis for the high moment elements using 2D elements. The nodal moment loads in the localized detailed analysis are extracted from the general analysis results.
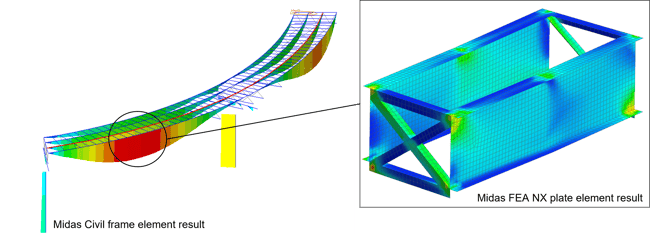
Figure 4. General analysis using 1D element and using its element force-moment results as initial loads for the 2D detailed analysis.
- Two-Dimensional Elements
To solve two-dimensional (2D) problems, 2D elements are needed. Similar to how stiffness matrix is constructed for 1D elements as shown in equation 6, 2D elements’ stiffness matrix can also be constructed from shape function and interpolation,
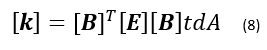
where again, [k] is the stiffness matrix, [B] is the strain-displacement matrix obtained from the shape functions, [E] is the constitutive matrix, t is the thickness of the element, and A is the area of the element.
Common 2D problems include plane stress, plane strain, shell, axisymmetric solid, geogrid 2D, and gauging shell elements. Plain strain and axisymmetric solid elements are 2D shape elements, but they are used to express 3D stress states [2]. The common 2D element shape used is the triangular element with 3 nodes, shown in figure 5a, this type of element is called a constant strain triangle (CST) because, in stress analysis, a linear displacement field produces a constant strain field [1]. The CST elements do not work very well, because the “locking” effect can make the mesh overly stiff [3]. Even though refining the mesh can help with the accuracy, it also does increase the analysis solving time. The inaccuracy due to “locking” can be improved with the 6 node triangular elements. As shown in figure 5b, they have middle nodes between the vertices. 6 node triangular elements are also known as linear strain triangles (LST) or quadratic triangles.
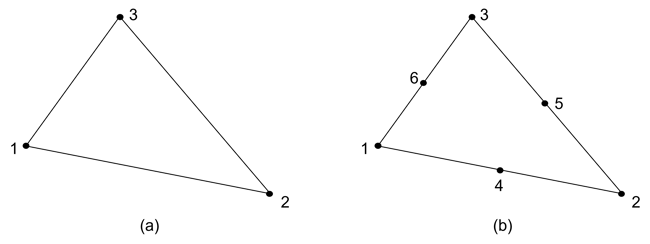 Figure 5. (a) Constant-strain triangle element, (b) Linear strain triangle element.
Figure 5. (a) Constant-strain triangle element, (b) Linear strain triangle element.
A simple but less used 2D element is the 4-node rectangular element (Q4) whose sides are parallel to the global coordinate systems. This system is easy to construct automatically but it is not well suited to approximate inclined boundaries [4]. The Q4 elements experience the same “locking” effects as the CST elements, however, the issue can be improved with quadratic rectangular elements (Q8, Q9) by adding mid edge nodes.
- Three-Dimensional Elements
As shown in figure 6(a), tetrahedron has 4 nodes and is the most basic 3D finite element. Figure 6(b) shows a pentahedral (pyramid) element, figure 6(c) shows an 8 node rectangular solid element (Q8), and figure 6(d) shows an 8 node hexahedral isoparametric element.
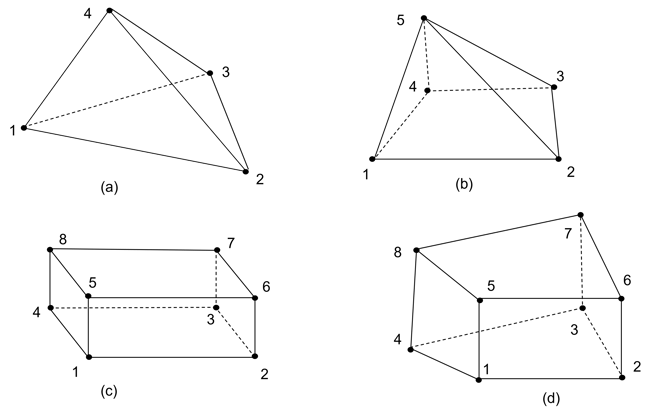
Figure 6. (a) 4 node tetrahedron element, (b) 5 node pentahedral (pyramid) element, (c) 8 node rectangular solid element, d) 8 node hexahedral isoparametric element.
Similar to rectangular Q4 elements and CST elements, Q8 also has the disadvantage of shear locking. Also similar to Q4 elements, Q8 rectangular solid elements are difficult to mesh irregular geometries, especially for geometries with varying mesh densities. To reduce shear locking, adding mid-edge nodes to the Q8 element would help, and making the elements isoparametric will help with meshing flexibilities. Isoparametric formulation permits quadrilateral and hexahedral elements to have non-rectangular shapes [1]. When combining the two efforts, adding mid-edge nodes to the linear isoparametric hexahedral elements would make them more versatile and produce better analysis results.
3D geometries are needed to perform 3D mesh and they come from CAD models, which take longer and more effort to produce. Furthermore, analysis containing 3D elements usually contains more nodes and elements thus would take longer to solve. 2D analysis, however, requires less time to mesh and less time to solve. The 2D analysis also provides a more sufficient amount of structural information than 1D analysis and produces results close to 3D analysis. However, 2D analysis can only replace 3D analysis when structures can be represented by plate elements. When a structure is more complex, as shown in figure 7, 3D elements need to be used.

Figure 7. A lug and pin model.
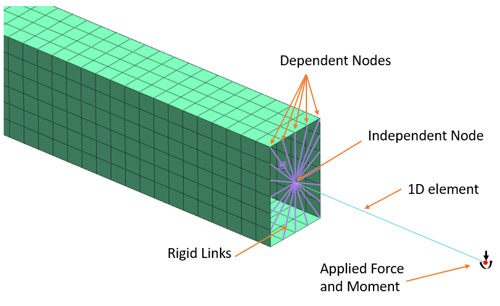
Engineers sometimes model structural elements using combined 1D/2D/3D mesh to take advantage of the benefit of each type of element while saving analysis time, as shown in the bridge model in figure 8.
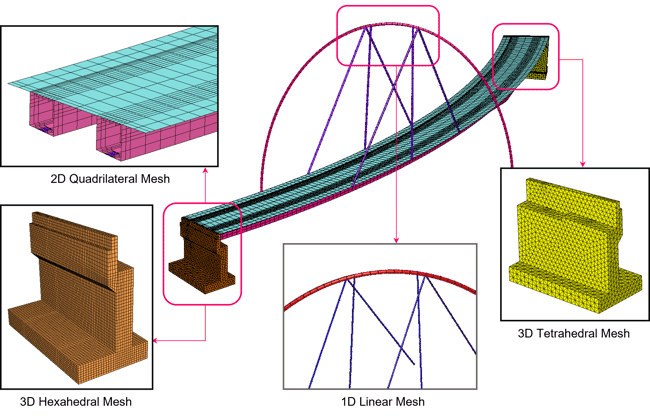
Figure 8. A bridge model utilizing hybrid element types with merged nodes at the element boundaries
References:
[1] R. Cook, D. Malkus, M. Plesha, R. Witt, Concepts and Applications of Finite Element Analysis, Fourth Edition, 2001, John Wiley & Sons Inc., New York, NY.
[2] Midas Information Technology, Analysis Reference Midas FEA NX, Chapter 3, 2021.
[3] Th. Zimmermann, S. Commend, Stabilized Finite Element Applications in Geomechanics, Laboratory of Structural and Continuum Mechanics, Department of Civil Engineering Swiss Federal Institute of Technology, 2001, Lausanne-EPFL, Switzerland.
[4] S.S. Bhavikatti, Finite Element Analysis, 2005, New Age International Limited, New Delhi.
https://www.midasoft.com/bridge-library/civil/products/midasfeanx
jsun@midasoft.com

Add a Comment