Streamlining Initial Cable Tension in Cable Stayed Bridges: The Midas Approach

Author: MIDASoft
Publish Date: 7 Nov, 2023
|
Summary: Determining the initial cable forces in cable-stayed bridges is a critical step in ensuring the structural integrity and stability of these magnificent engineering marvels. This article explains the methods and techniques engineers employ to calculate and set the initial cable forces accurately. It's showing how Midas Civil aids in the effortless analysis of cable-stayed bridges. |
An Introduction to Cable Stayed Bridges
A cable-stayed bridge is a structural system that effectively combines cables, girders, and the pylon into an esthetically pleasing structure.The pre-tensioned cables reduce the moments coming onto the girders acting like intermediate supports, and thus, engineers can go for longer spans that balanced cantilever bridges cannot afford.
The concept seems simple, but calculating the cable forces becomes complicated, and in the past, the initial pretension was determined by experimental values, trial-and-error methods etc.
Are you curious about how these elegant structures are structurally analyzed? Keep reading.
Different Methods of Determining Initial Cable Forces
As mentioned above, the dominant issue of the design and build of a cable-stayed bridge is to compute and achieve the initial equilibrium configuration at the completed state. Let’s check out different methods for calculating the initial cable forces for obtaining the desired behavior.
The initial equilibrium configuration of cable-stayed bridges is the equilibrium position due to dead load and tension forces in the stay cables. The cable pretension should be optimized to reduce the moments in the tower and girders.
Figure 1: Russky Island Bridge in Russia; World's tallest cable stayed bridge (Analysed using Midas)
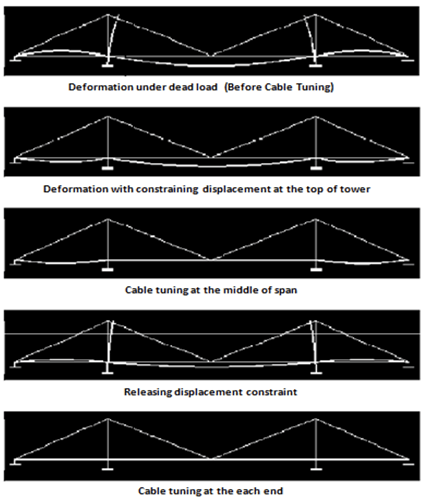
Traditional “Zero Displacement” method
This method is valid when there is no large inclination in the longitudinal girder, and the horizontal component of cable force's effect on the beam is less. In this method, vertical displacement is restrained at the cable anchorage position so that the girder can be idealized as a continuous beam.
Procedure for cable force optimization
- Assign roller supports to the cable anchorage position of the deck without cable
- Apply dead load and obtain the reactions at the roller support
- Calculate the horizontal component of cable force from the reactions and apply the loads as nodal loads in the main girder and pylon.
- Cable forces are then tuned to get the optimum moment range
- For horizontal cable force tuning, fix the vertical & horizontal displacement of the tower
- Apply prestress force to have zero vertical displacement at the mid-span
- Release the horizontal displacement of the tower and adjust the prestress force to have “0” horizontal displacement at the tower and vertical displacement at the girder midspan.
Figure 2: Zero Displacement Method
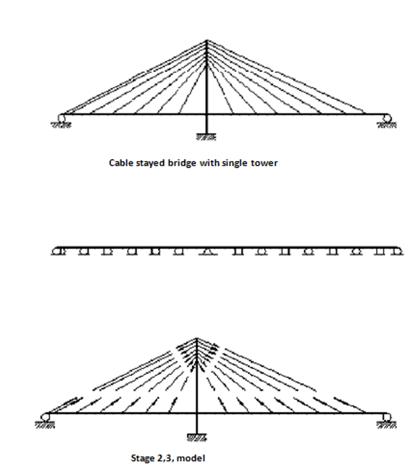
Force Equilibrium Method
This method is valid when there is a considerable inclination in the longitudinal girder and the horizontal component of cable force's effect on the beam is large. Thus, the effect of horizontal cable force is considered while calculating the initial cable forces.
Procedure for cable force optimization
- Assign fixed supports to the cable anchorage position of the deck and tower without the cable
- Apply dead load and obtain the target moments
- Enter the cable forces to have the target moment distribution after deleting the supports
- Optimize the cable forces to achieve zero moments in the tower
- The sagging effect of the cable is ignored, and the pretension in the cable at both ends is assumed to be identical
- Assume that the bending moments of the girders are affected by cables connected to the girders. In contrast, the bending moments of the tower are affected by cables connected to the tower only.
Figure 3: Force Equilibrium Method
Force Method
In the force method, we can assume the member force by converting the structure as determinate structure. Using the member forces due to live loads to obtain member forces due to dead loads. Member force can be efficiently determined considering the material properties.
Procedure for cable force optimization
- Calculate the moment distribution due to dead load without cable pretension
- Assume the structures as a determinate structure
- Assume the moment of the value in the hinge position
- Determine cable pretension to have this moment distribution
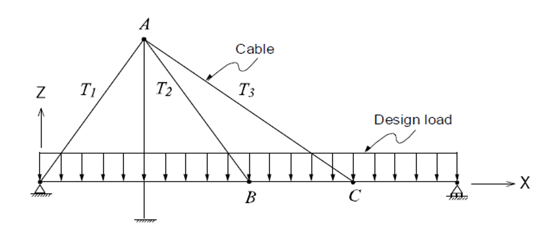
Influence Matrix Method
In this method, to determine the unknown loads for each stay cable and to achieve an ideal state, a unit pretension load is applied for each cable. Performing a linear analysis - the method determines the influence on the structure due to each unit's tension load. Furthermore, the structural restrictions for e.g., moment or displacement values, which are realized through the load factors in the combined load case, must be defined.
Figure 4: Influence Matrix Method
The Midas Touch - Cable force optimization in Midas
Engineers across the globe have realized the Midas touch of Midas Civil in solving complicated bridges, such as the Russky Island Bridge in Russia, the tallest cable-stayed bridge in the world, the Sutong Bridge in China, the second-longest cable-stayed bridge in the world, and many other wonders around the world.
Let's see how initial cable forces are calculated in Midas Civil and how the software helps the engineers optimize the cable forces efficiently in the nick of time.
Figure 5: Sutong Bridge, China; World's second longest cable stayed bridge (Analysed using Midas)
Unknown Load Factor
Using the Influence Matrix Method, this function optimizes cables' tensions at a cable structure's initial equilibrium position. The program can calculate the initial cable force by inputting restrictions such as displacement, moment, etc. and satisfying the constraints.
Procedure for cable force optimization
- Define the constraints and obtain the Unknown Load Factors for the Pre tension Forces
- Determine the Pretension Force by multiplying those factors with the assigned Pre tension Loads
- Change the Pretension Forces with the new ones (obtained in step 2)
- Perform the Analysis
- Check whether the constraints are satisfied with modified pretensions
- If not, then determine the Unknown load factors again and repeat steps 2 to 5 until you get the constraints satisfied after static analysis (step 5).
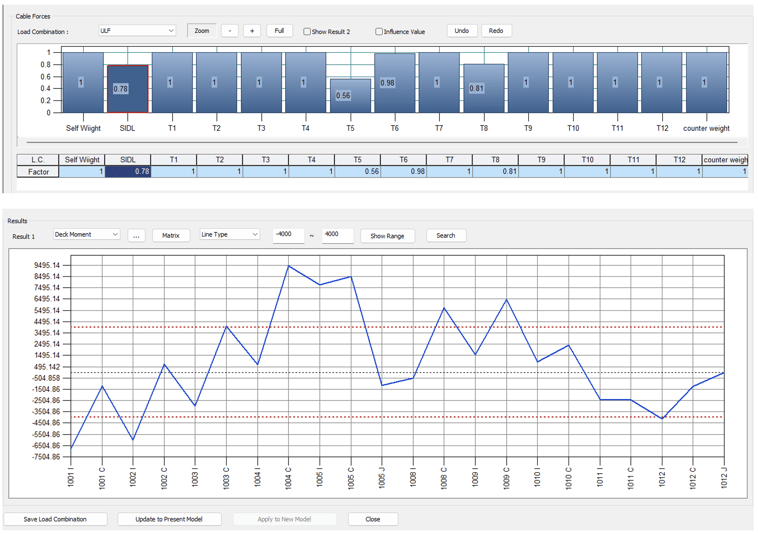
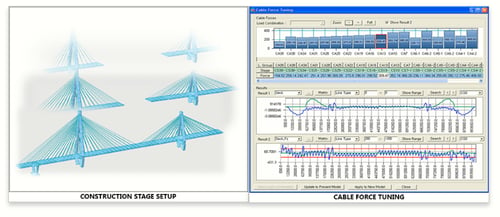
Figure 6: Before & After Cable Force Tuning
The 'Unknown Load Factor' function in Midas Civil calculates the initial pretension that needs to be applied to the cables for a cable-stayed bridge. However, with the 'Unknown Load Factor,' the designer cannot achieve the desired initial pretension in a single attempt. The designer should perform multiple iterations, fine-tuning the pre tension using the influence matrix to obtain the initial pre tension that results in the desired bending moments and deformations.
Cable Force Tuning
Cable Force Tuning' in Midas Civil is a function that makes the iteration process required for bridge design easy. The feature allows the user to adjust the cable force and check the girders' displacements or the pylon in real time without reanalyzing. Click here to learn more about cable tuning in Midas Civil.
Figure 7: Cable Force Tuning in Midas Civil
No Time for Trial & Error: The Future of Cable-Stayed Bridges
Now, bridges are longer and more complex than ever before, and the world is moving faster. We cannot afford to waste time solving the indeterminacies of cable-stayed bridges through trial-and-error methods.
With Midas Civil at their disposal, engineers can confidently begin designing and building cable-stayed bridges since the software simplifies the most complex indeterminate structures time-bound.
As we look to the future, Midas Civil continues to play a pivotal role in shaping the skylines with safer, more efficient, and truly iconic cable-stayed bridges worldwide.
Stay tuned for more exciting bridges in the upcoming blogs.




Add a Comment