Expert Tip: Moment of Inertia for Cracked Circular Concrete Section

Overview

Sometimes we need tiresome calculations, even though they are not critical nor difficult, but they are essential, and they take time if we do not have proper tools. One of these is the moment of inertia calculation for cracked, circular concrete sections. We need this calculation when we perform service stress checks for flexure and deflection checks.

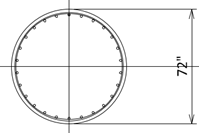
f’c = 3.5 ksi, 2 in. cover, #5 spiral (d = 0.625 in.), 1% reinforcement with #11 (d = 1.410 in.) rebars

In the symmetrical reinforcement sections, each rebar location needs is not considered, and we can assume the rebars as a ring.

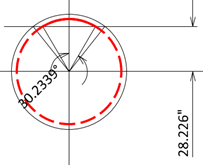
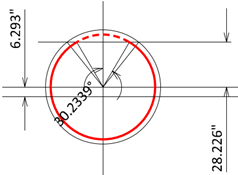
D1 = 72” – 2(2” + 0.625” + 1.410”/2) = 65.34”

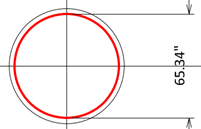
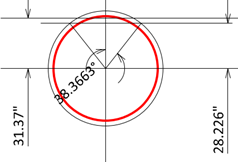
Step1) Assume neutral axis location

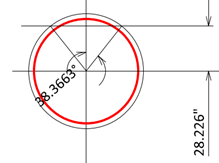
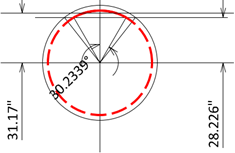
Assume the neutral axis for the cracked section is located 28.226” from the circle center.

r cosα = (36”) cosα = 28.226”

α = 38.3663° = 0.6696 rad

Actually, it is more common and convenient to assume the angle α first then calculate the neutral axis location (r cosα).

Step2) Calculate compress zone concrete area

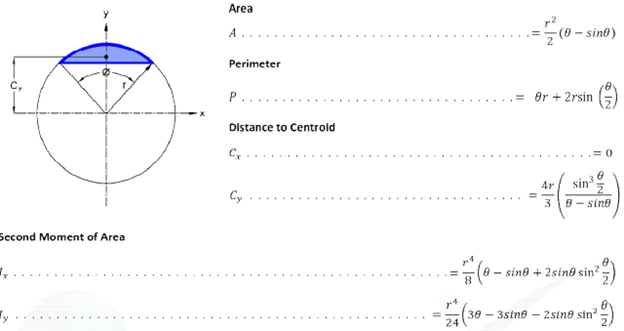
Step3) Calculate compression rebar area

r1 cosα1 = r cosα=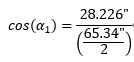 

α1 = 0.5277 rad = 30.234°

n = (29000 ksi)/(1820√3.5ksi) = 8.517

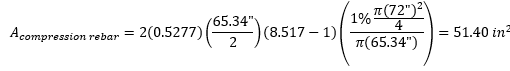
Step4) Calculate tension rebar area

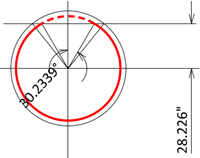
α1 = π - 0.5277 rad = 2.614 rad = 149.8°

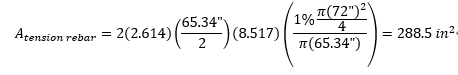
Step5) Check assumed neural axis location

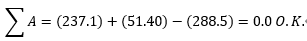
Repeat Step 1 to Step 5 until this equation is satisfied.

Step6) Calculate the moment of inertia for the neutral axis

Compression concrete

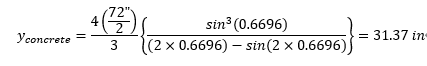
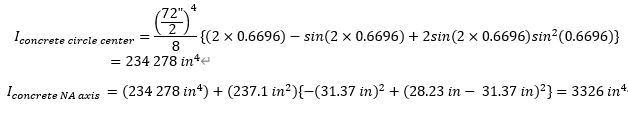
Compression rebar

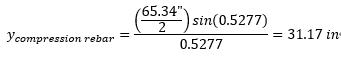
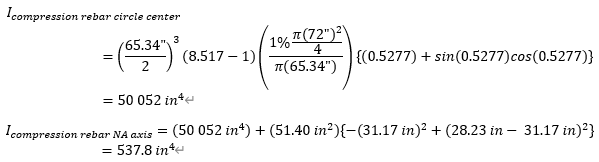
Tension rebar

Step6) Check

Moment of inertia from the rebars can be checked easily. The total number of rebars is assumed as 26 EA.

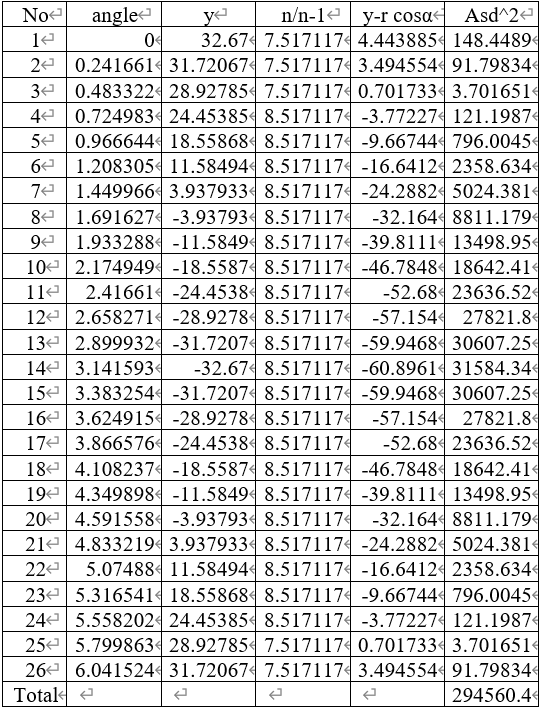
Ad² = (1%)(1/4)π(72 in.)²(294560.4 in⁴) = 461 271 in⁴

573.8 in⁴ + 460 732 in⁴ = 461 270 in⁴    O.K.

Either way results in the same results (however, the closed-form is always looking neat, somewhat more professional).

The corresponding excel sheet is attached.