Expert Tip: Analysis of Suspension Bridges 5

Author: Seungwoo Lee, Ph.D., P.E., S.E.
Publish Date: 29 Aug, 2023
Dr. Hirai was a Japanese engineer, professor, and researcher. In 1940, Dr. Hirai went to a movie theater and watched the news about the failure of the old Tacoma bridge. He was very inspired and started his research on wind engineering for suspension bridges by himself. His papers had been published since 1942, but they were rarely introduced into the Western world because Japan was isolated during World War II.
The basic step of wind engineering is eigenvalue analysis, and his method is as follows.

Model view
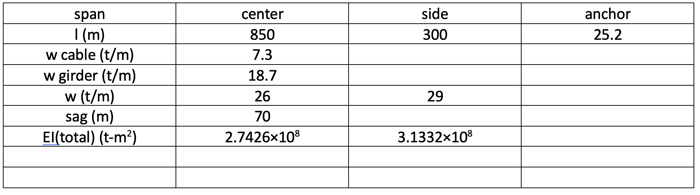

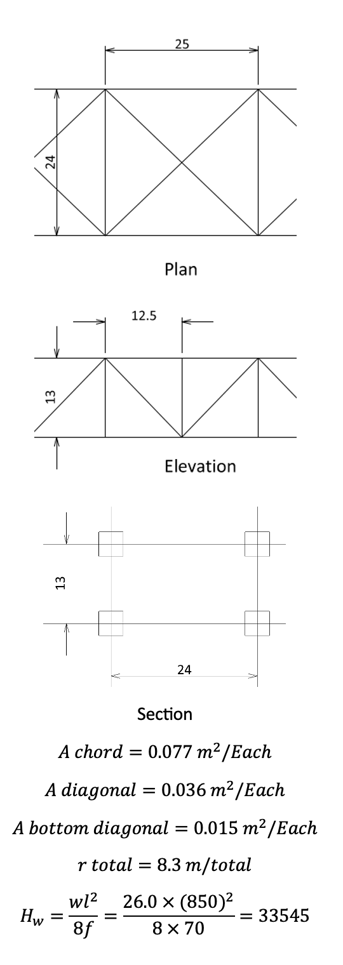
Analysis of Suspension Bridge - Vertical vibration-Asymmetrical mode
Assumed shape function
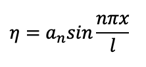
Center span
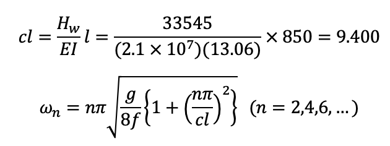
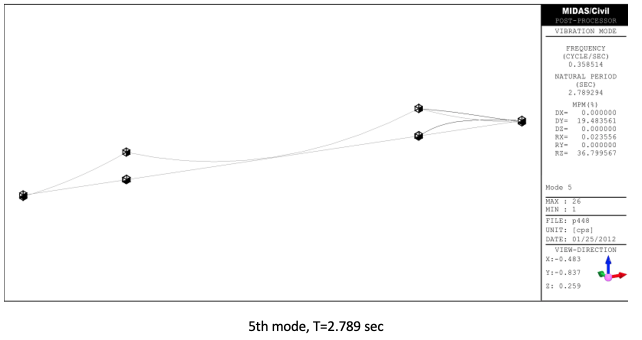
Analysis of Suspension Bridge - 2nd Mode
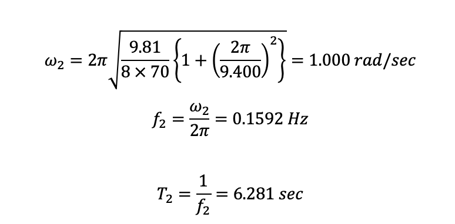
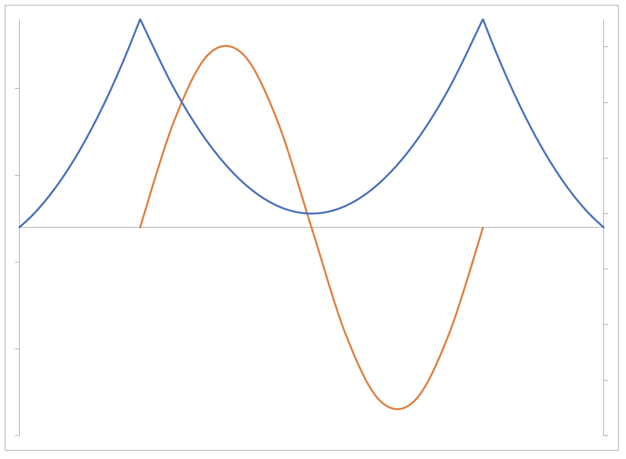
Vertical, Asymmetrical, 2nd mode, T=6.821 sec
Analysis of Suspension Bridge - 4th Mode
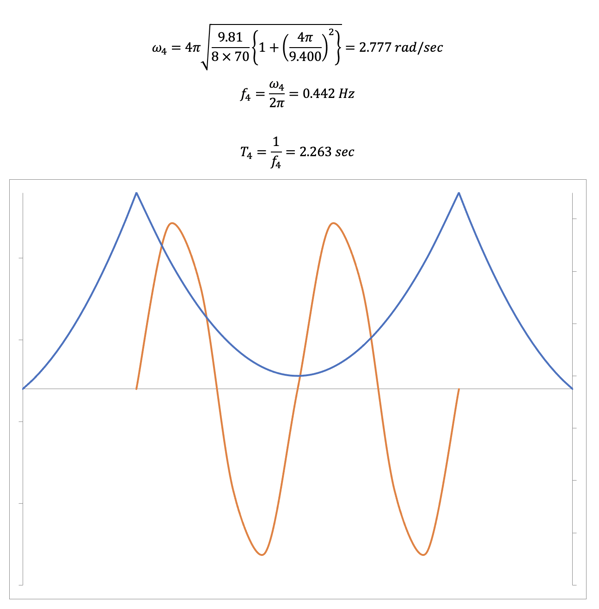
Vertical, Asymmetrical, 4th mode, T=2.263 sec
Sider span
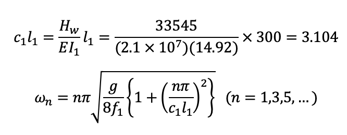
Analysis of Suspension Bridge - 1st Mode
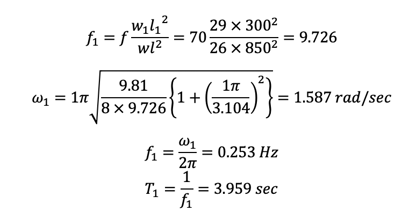
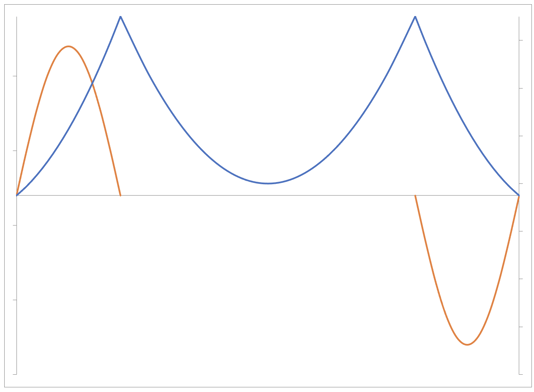
Vertical, Asymmetrical, 1st mode, T=3.959 sec
Analysis of Suspension Bridges - Vertical vibration-Symmetrical mode
Frequency equation
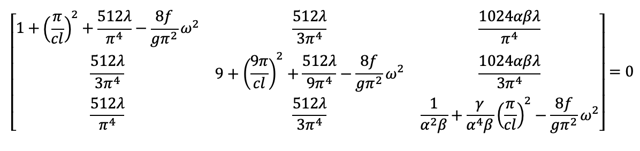
Assumed shape function

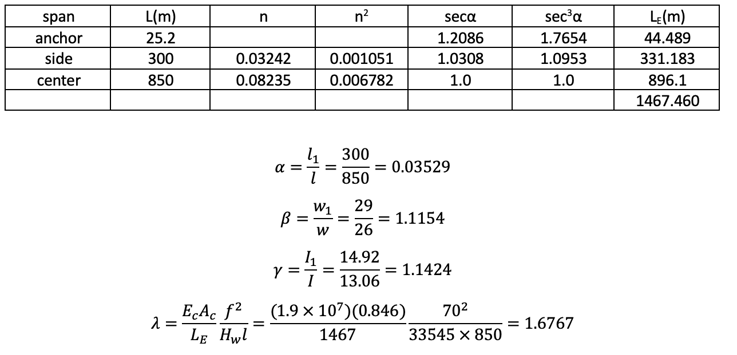

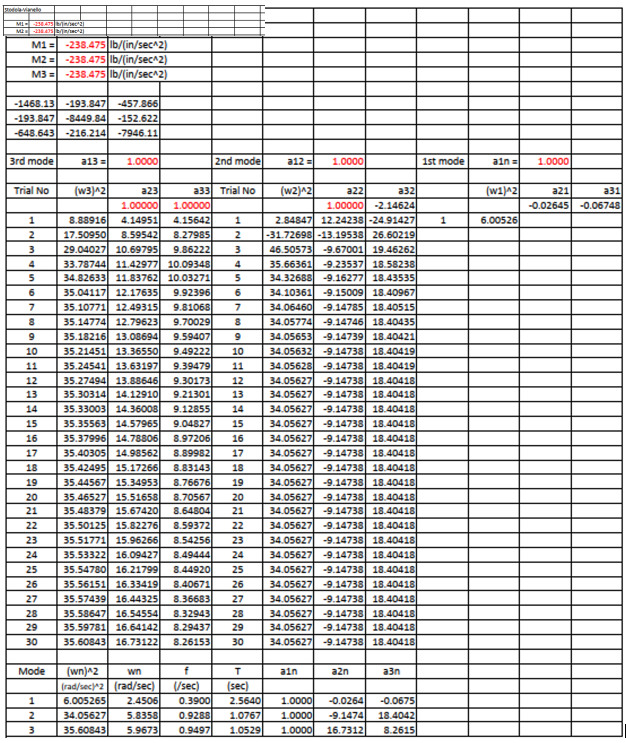
There are many ways to solve this frequency equation. The author’s favorite is the Stodola-Vianello method.
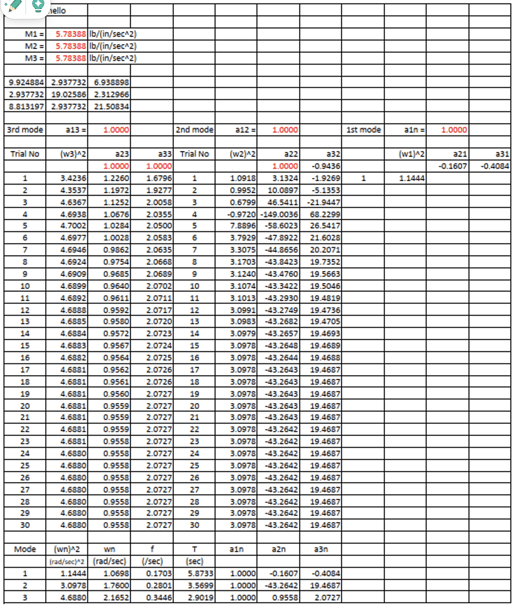
Vertical vibration-Symmetrical mode - 1st mode
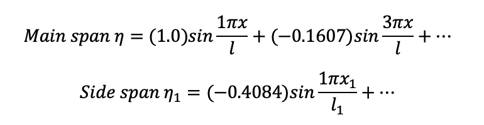
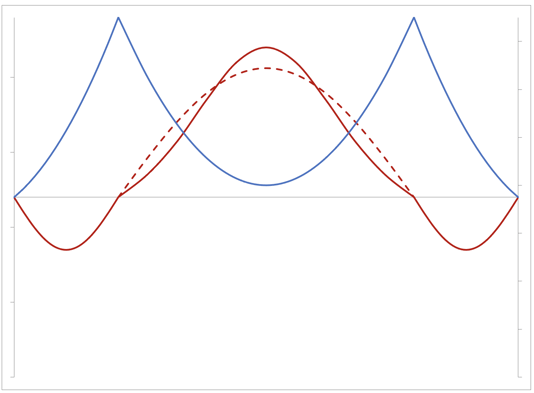
Vertical, Symmetrical, 1st mode, T=5.8733 sec (dashed line shows the 1st term)
Vertical vibration-Symmetrical mode - 2nd mode
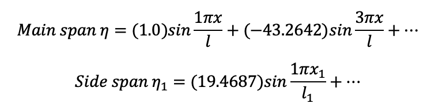
Vertical, Symmetrical, 2nd mode, T=3.5699 sec (dashed line shows the 1st term)
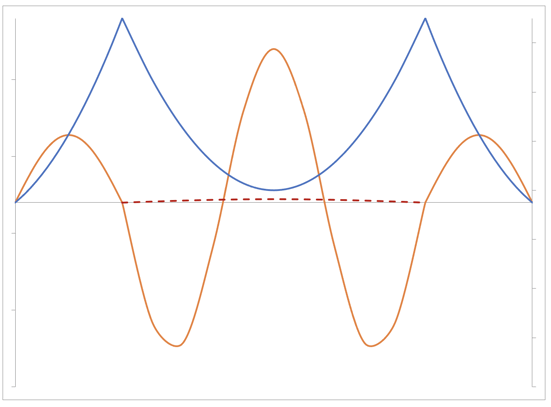
Vertical vibration-Symmetrical mode - 3rd mode
Vertical, Symmetrical, 3rd mode, T=2.9019 sec (dashed line shows the 1st term)
Torsional vibration - Torsional rigidity

Waring torsional rigidity
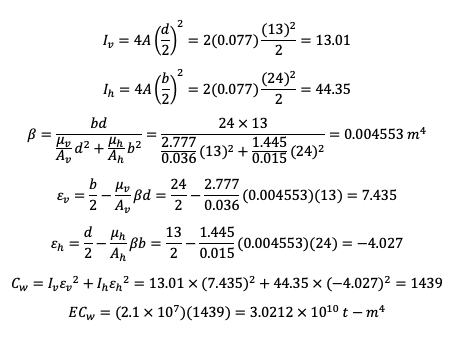
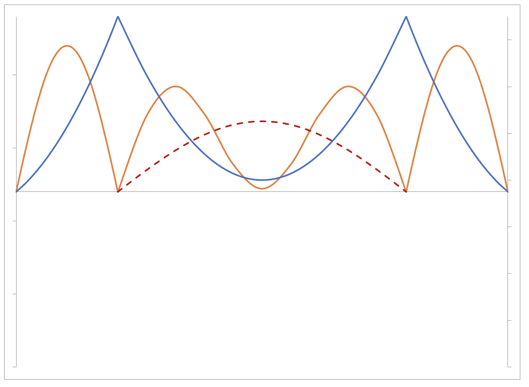
Torsional vibration-Asymmetrical mode
Assumed shape function
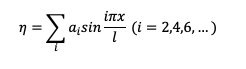
By energy methods
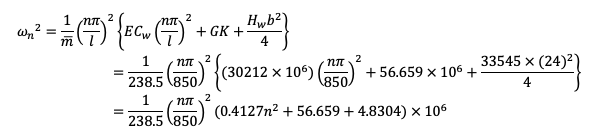
In the first term, the warping term, and the third term, effects from cable tension are negligible in the lower modes as can be expected.
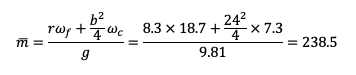
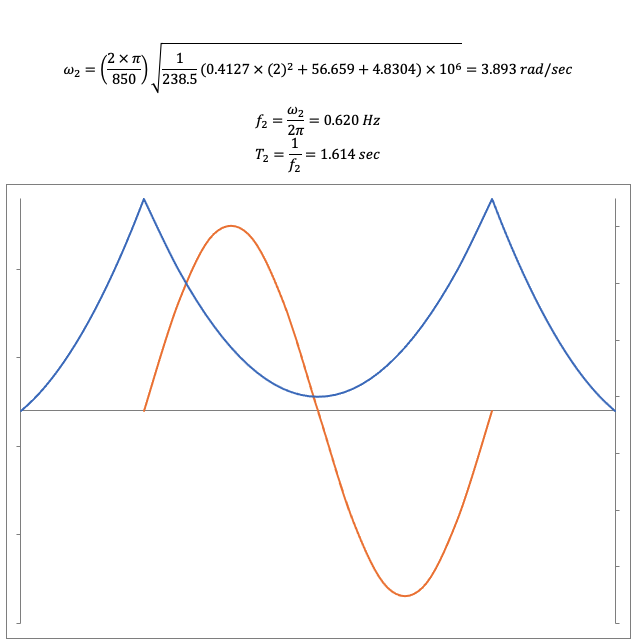
Torsional, Asymmetrical, 2nd mode, T=1.614 sec (red line shows rotational angle)
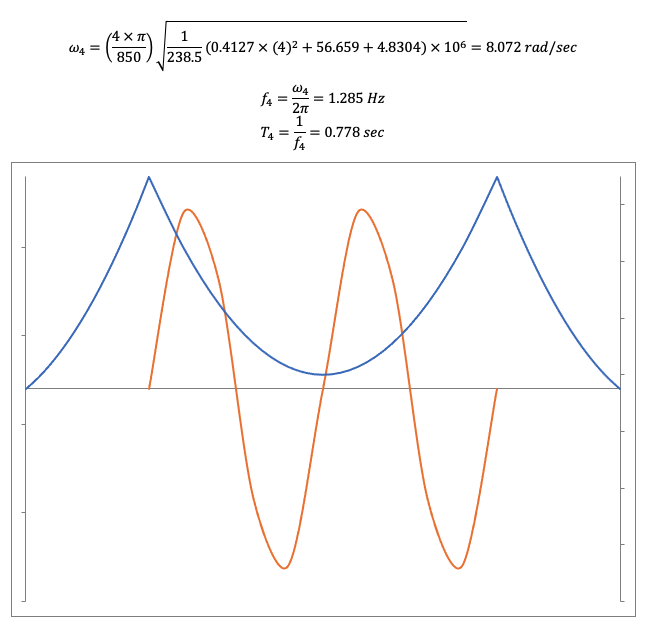
Torsional, Asymmetrical, 4th mode, T=0.778 sec (red line shows rotational angle)
Torsional vibration-Symmetrical mode
Assumed shape function
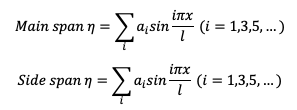
Ritz’s methods, frequency equation is,

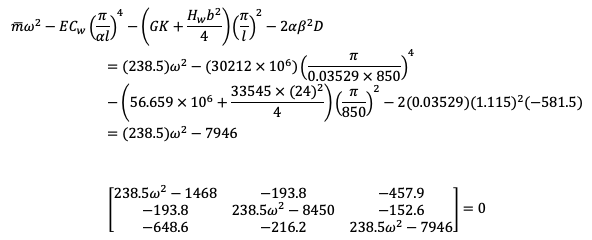
Solve frequency equation by Stodola-Vianello method
1st mode
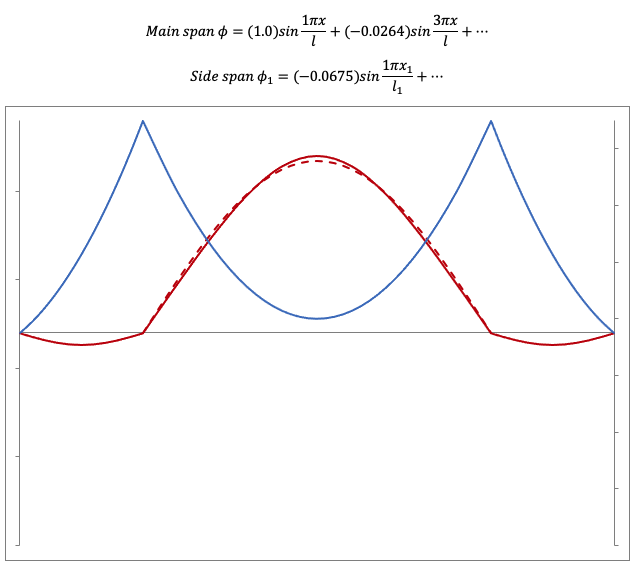
Torsional, Symmetrical, 1st mode, T=2.5640 sec (dashed line shows the 1st term)
3rd mode
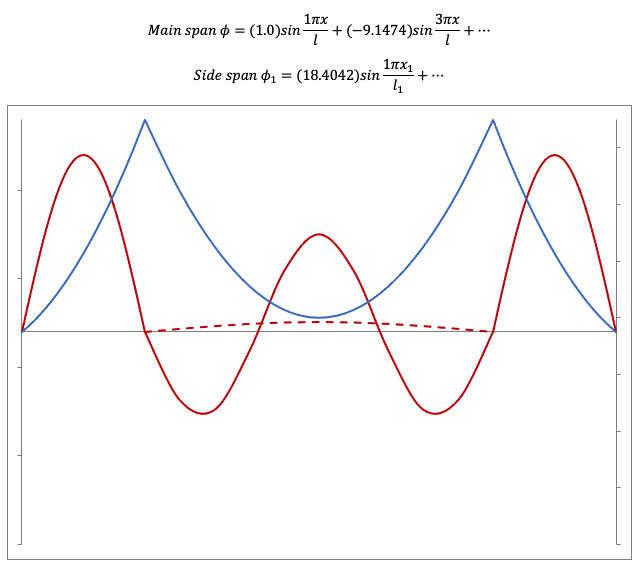
Torsional, Symmetrical, 3rd mode, T=1.0767 sec (dashed line shows the 1st term)
5th mode
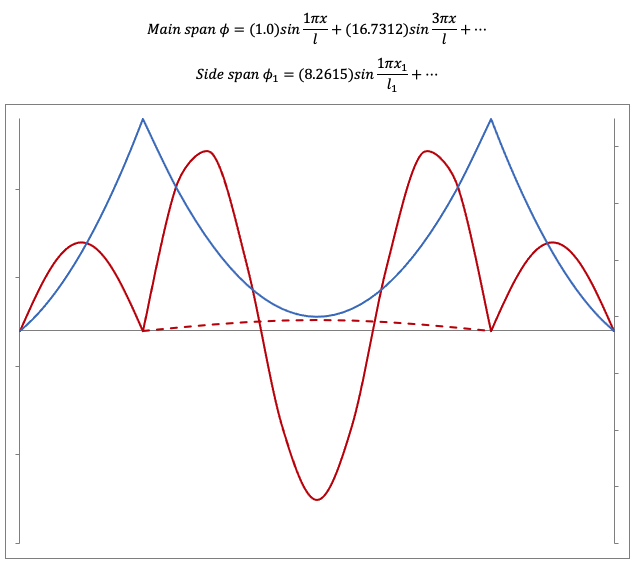
Torsional, Symmetrical, 5th mode, T=1.0529 sec (dashed line shows the 1st term)
Transverse vibration
Assumed shape function
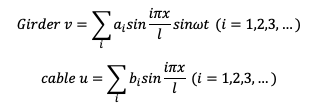
Frequency equation
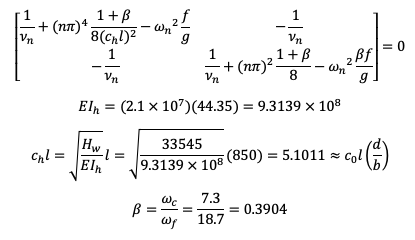
1st mode

In-phase

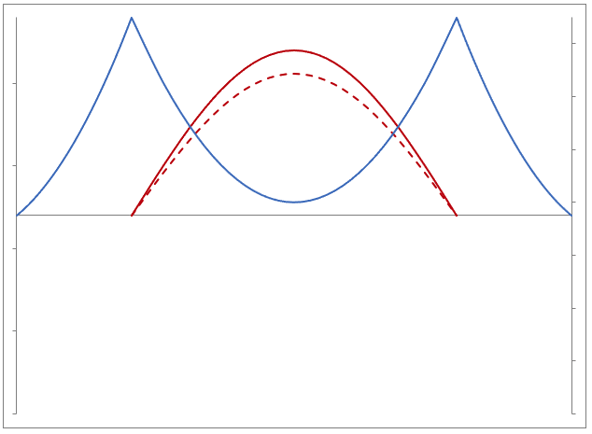
Transverse, 1st mode, in-plane, T=13.31 sec (dashed line shows cable)
Out-of-phase
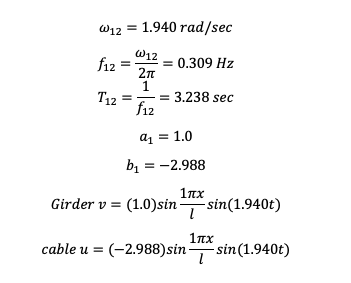
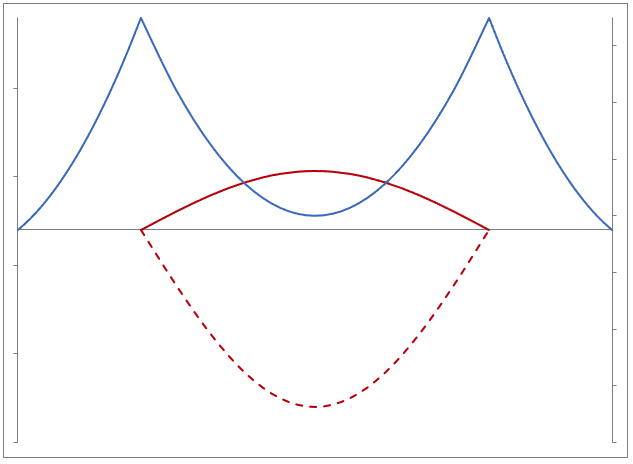
Transverse, 1st mode, out-of-plane, T=3.238 sec (dashed line shows cable)
2nd mode

In-phase
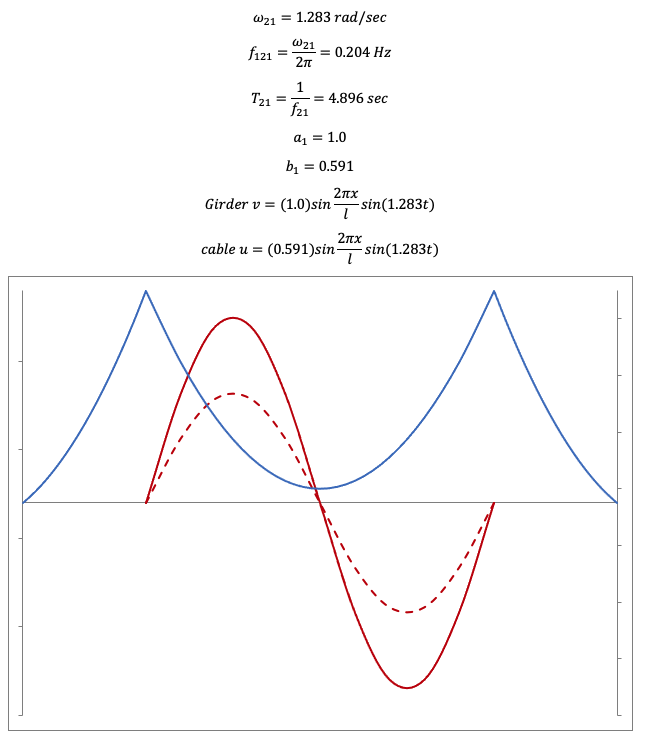
Transverse, 2nd mode, in-plane, T=4.896 sec (dashed line shows cable)
Out-of-phase
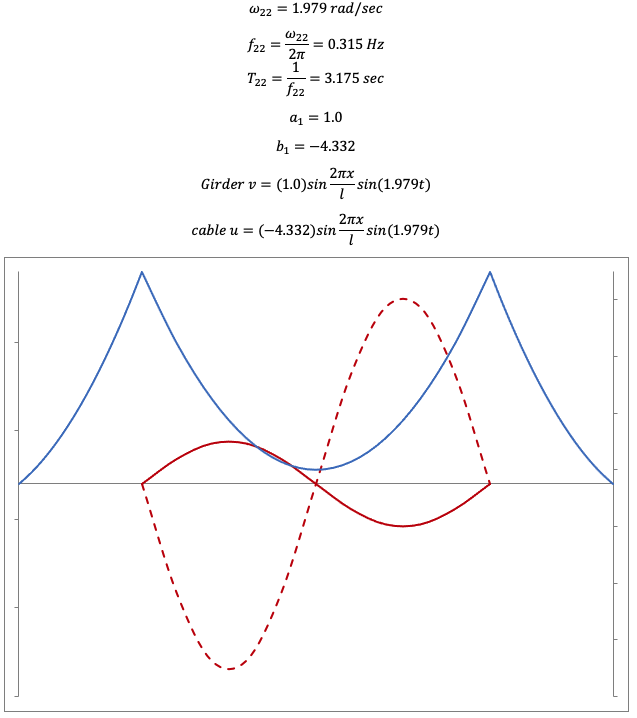
Transverse, 2nd mode, out-of-plane, T=3.175 sec (dashed line shows cable)
Eigen value analysis results from classic methods and MIDAS
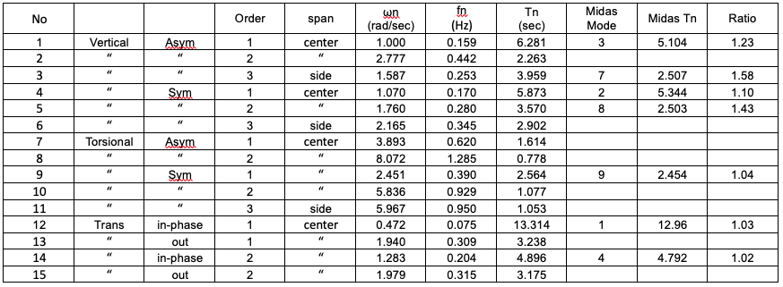
For lower modes, transverse modes are very well matched, vertical modes have 10% to 23% differences. In the vibration analysis, only some lower modes are important.
From the author’s view, this classic method from Dr Hirai gives very reasonable results and it is an excellent tool to check the computer output. After we make a simple Excel, it is very easy to check for other geometry and/or loadings which takes some time with displacement methods.
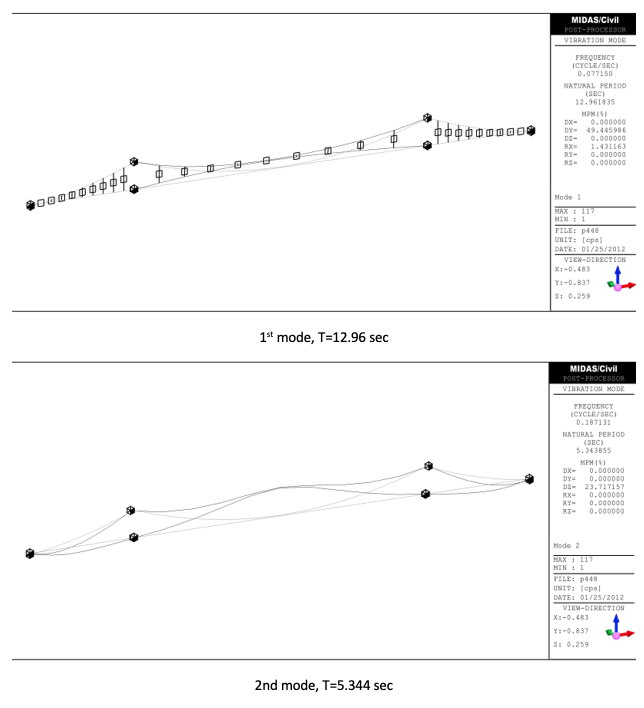
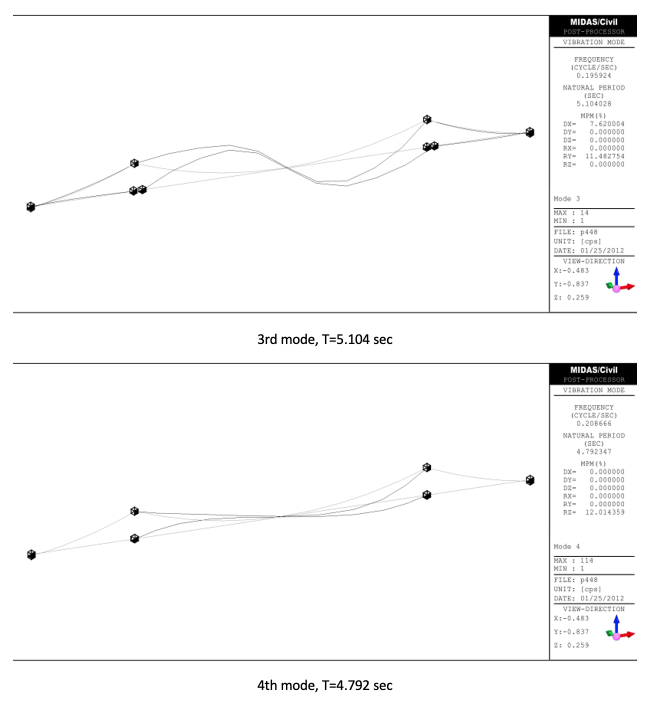
Finally results from MIDAS are attached for the lower five modes.
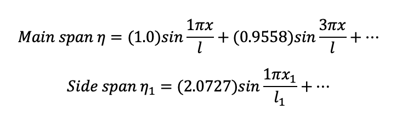



Add a Comment